株式会社東栄 磁気応用部
サイトはこちら
磁気の話のはじめに
1.電荷と磁荷
2.磁気モーメントと磁性材料
3.反磁界と磁化特性
4.強磁性体
5.軟磁性材料
6.磁性材料と高周波
7.微粒子材料
8.磁気の計測
9.スピントロニクスについて
補足Ⅰ 多層膜の軟磁性
補足Ⅱ 薄膜インダクタ
補足Ⅲ 微粒子の透磁率
補足Ⅳ も一度反磁界
参考文献
磁性材料・磁気工学入門
© 2019 Yutaka Shimada

3. 磁性材料の反磁界と磁化特性
3-1. 磁化曲線と反磁界
この話も、やっと「反磁界」まできました。反磁界は、電気工学と磁気工学の最大の相違点と言えます。これからの話には、陽に陰に反磁界が語られます。反磁界がどう効いているか、磁気素子の材料と形を見て、反磁界の影響が直感的にわかるようになれば、磁気工学の中心概念を獲得したと言っていいと思います。
ここでは、前章のような、磁気モーメントが自然に揃った永久磁石的材料でなく、外部磁界を印加することによって磁化( I )が増えていく(磁気モーメントの方向が揃っていく)材料、つまり軟磁性的材料の場合を考えます。
図3-1-1の上段は、透磁率の高い磁性材料(軟磁性材料)の円環(磁気コア)で、励磁用の巻線N があります。 I は、磁気モーメントのベクトル成分が、ある方向にどれだけ大きいか、単位体積あたりで表した量です。I は磁界H によって増えて行きますが、全ての磁気モーメントが磁界の方向を向いてしまうと、磁気飽和の状態になります(厳密には正しくないですが、磁気工学的にはOK)。飽和磁化を Is 、飽和磁界を Hs とします。I と H の関係は、磁化曲線、磁化過程、B-Hカーブ、などいろいろな呼び方があります。
一般的な教科書には、「磁界の強さによってその磁化過程は変わり、磁界の増加に伴って、初磁化過程、磁壁移動領域、磁化回転領域、飽和領域となる」と説明されておりますが(参考文献3—1)、今は、このような磁化の過程(磁化機構とも言う、後で出てくる))は忘れて、磁界が増えると I も透磁率μe を比例定数として増えると言うことだけを仮定して、I = μ0H + I (H) の磁界中の変化と反磁界との関係のみを取り上げます。つまり、ここで考察する反磁界は、第2章の反磁界が永久磁石的に磁気モーメントが揃っていることを出発点としたのに対し、磁気モーメントが外部磁界で揃っていく過程に反磁界を取り入れまます。
まずは、「磁気回路」の話をします。
図3-1-1の上図で、巻線に励磁電流(直流電流)i (アンペア)を流すと、N × i は起磁力になり、これによってコア内全周にわたって磁界 Hi が分布し、起磁力はHi とコア長さ( lc )の積に等しくなり、N × i = Hi × lc となります。その関係から、
図3-1上段の右には、模式的な磁化曲線(高い透磁率( μe )の場合)を描いてあります。透磁率が磁界に係わらず比例定数としているので、Is まで直線的に磁化が増加します。また、透磁率が高いので弱い Hi で Is(飽和磁化) に達します。また、μ0 << μe なので、μ0Hi による B の増加は、図に表していません。
次に、図3-1-1下段の様に一部を空芯(エアギャップ lg )にして、同じ大きさの磁束密度B を作ることを考えます。この時には、コア内の磁界 Hi とギャップ内の磁界 Hg の間には大きな差が出来ます。これは、第1章と同じですが、同じ B を作るためには、透磁率 μ0 のギャップ内には強い磁界が必要なためです。励磁電流も増加して i' になり、起磁力の関係式は、
(3-1)、(3-3)のような表現は、起磁力(N×i )、および(各部の磁界×各部の長さ)の総和 の関係を記述する「磁気回路の式」で、電気回路に対応する便利な式です。この式によって、lg がある時に必要な励磁電流 i' がわかります。ところで、反磁界はどこに行ってしまったのか、、、、
実は、反磁界は(3-3)で明解に表現されています。以下に、それを説明します。
図3-1-2には空間に正負の電荷(a)、N、S の磁極(b)が配置されています。(a)は、正、負の電荷の間にある電気力線で,接線が電界 E の方向です。この曲線の一つに沿って電界を積分すると、二つの電荷の電位差(電圧)V になります。(b)は、磁極 N と S の間の磁力線で接線が磁界 H で、同じく積分すると磁位差(起磁力)K になります。それらの積分値は、どの経路を選んでも同じで、
これを、図3-1-1のようなリングコアを模した磁力線に使って見ると、図3-1-3のようになります。コアのギャップ面にNとSがあると、その磁位差は、lg あるいは lm(= lc - lg )に沿った積分値になり、コア内部の反磁界はHd 、ギャップ内は Hg になるから、
つまり、反磁界 Hd を克服するための起磁力 Hdlm は、ギャップ内(磁性体から見て外部)に磁界を作るための起磁力 Hglg に書き代えることができるのです。これが、式(3-3)の lgHg で、コア内の反磁界×コア長を書き代えた分です。要するに、反磁界×磁性体長さとは、磁性体(この場合はコア)の外部(ギャップ)に磁束を作るために必要な、余分な起磁力である、ということになります。ですから、(3-3)のような磁気回路の式を使う場合、つまり、磁性体内部だけでなく、外部の磁束分布も入れた磁気エネルギーの全体系を考える時には、反磁界は自動的に外部の磁束経路に沿った磁界で表されているので、忘れていいのです。別の言い方をすれば、磁気回路は、全空間にわたって終わりのない磁束の通路の全部を起磁力という形で入れているからです。外部の全てを考慮した磁気回路に磁性体内部の反磁界を改めて入れてしまうと、double count になってしまいます。一方、「教科書的な反磁界」は磁束通路の全部を考えずに材料内にだけを見て、外部磁束に必要な起磁力を反磁界として材料内に組み込んでいるわけですが、一般に、このあたりの説明が不足していることが、混乱の原因になりやすいのです。ただし、磁気回路では、内部と外部の磁束分布がほぼ同じ(図3-1-1)でないと、(3-3)のような簡単な表現はできません。
なお、磁気回路でなく、コアの反磁界係数を使うときには、コアの内部の形(図3-1-1の黄色の部分)の反磁界係数になるので、これは回転楕円体とは程遠い形では計算できませんが、図3-1-3の原理に基づいて、ギャップ部分の反磁界係数を楕円体に置き換えて計算する方法があります。「補足Ⅳ も一度反磁界」を参照してください。
さらに磁気回路の式を使ってみます。(3―1)、(3-2)より
であるから、
(3-5)、(3-6)より
ギャップがある場合には、(3—7)を使って、
この式を見ると、エアギャップができると、μ0 << μe なので i’ が急激に増えることがわかります。これに応じて図3-1右下の磁化曲線は傾斜が緩くなり、同じ B を作るために強い起磁力が必要になるわけです。
次に、ギャップのあるコアの実効的な透磁率( μeff )を考えます。
B は常に同じで、μeff は巻線Nから見た円周 lc のコアの実効的透磁率だから、(3―4)から、
(3-7)式は、ギャップができると μeff が急激に減ることを示しています。ギャップの影響については、もっと詳しい説明が(参考文献3-2)にありますが、以下では、コアに対するギャップの影響を簡単な計算式で考えて見ます。
まず、ギャップの無いコア(図3-1-1の上図)のインダクタンスLは、励磁電流 i 対する総磁束量× N ですから、コアの断面積を S として、
(3-7-2)によれば、コアの透磁率が高くて、ある程度のギャップ長があると、そのインダクタンスは、ギャップの空芯インダクタンスで予測できる、となります。(ただし、ギャップ内の磁束分布がコア内の磁束分布と同じ、と言う仮定が入るので、漏洩磁束の大きいギャップでは、修正が必要です。)つまり、励磁電流によって巻き線に溜め込まれた磁気エネルギーのほとんど全部は、ギャップ空間にある、と言うことになります。
次に、コアの素材の透磁率を μe = 1000、lg / lc = 1/10 と仮定すると、ギャップのあるコアの実効的な透磁率 μeff は、
ギャップの影響は非常に大きく、この計算では、lg / lc = 1/100 としても、μeff ≒ 100、さらに、lg / lc = 1/1000 になっても μeff ≒ 500 となり、わずかなギャップでも μeff を低下させます。実際には磁区ができて、単純な計算には合いませんが、影響の大きさはわかると思います。
このような磁気コアのギャップの影響は、実は、反磁界の効果そのものです。第2章では、磁性体/外部空間の界面での B の連続性のために、磁性体の端部近傍に、Hi = I / 2μ0 の反磁界ができると説明しましたが、それは界面近傍での話、現実の磁性体には(少なくとも)二つの端部に、それぞれ N、S が想定できるので、その N、S の分布と端面間の距離とによって磁性体内部の反磁界の分布が決まります。次のような例で、実際の材料の反磁界の影響の強さを感じることができます。
図3-1の上段、ギャップ無しのコアでは、磁束は全てコア内にあるため、反磁界はゼロです。下段のギャップありでは、B の連続性のためにギャップの両端面に N、S があり、巻線側から見ると、それに対応する反磁界以上の起磁力 Ni" が必要になります。図3-2は、さらにギャップが大きい場合です。(a)では、外部に広がる磁束の長さに対して磁性体が短くなり、さらに Ni' が増加します。(b)では、磁性体の長さと外部の磁束の長さは同程度ですが、磁束の総量が少なくなり、端部の磁極が少なくなりますので、Ni' は低下します。さらに(c)は平板、または薄膜です。磁化 I が面に垂直方向にあるとすると、磁性体の厚さは外部磁束の長さに比べて極端に短いですから、Ni" は非常に大きくなります。一方、I が面に平行(面内)にあると、端部の磁極量が非常に小さくなるので、反磁界も無視できる程度になります。つまり(c)では、I の方向(磁界印加の方向)によって、その磁化過程に極端な違いができます。このように反磁界は形状によって大きく異なりますが、同時に、同じ形状でも I が向く方向(磁界を印加した方向)によっても異なります。これは,おおざっぱに言って、ある方向の lg /(lc-lg) の比がどれだけ大きくなるか、に依存して反磁界の大きさが決まるからです。要するに磁化曲線も透磁率も材料の形と方向によって異なるので、形状磁気異方性といいます(あとで詳細説明予定)。
この反磁界と形状との関係は、是非理解しておかねばなりません。が、これまで長々と説明してきたように、磁束分布と形状の関係ですから、いろいろ複雑です。そこで、なるべく簡単に反磁界(反磁界係数)を見積もる方法(反磁界補正法)をいくつか紹介します。
①楕円形状への近似
今、楕円形状(回転楕円体)の磁性体を考えて、図3-3のように均一に磁化してみます。この時、楕円表面の仮想的な磁極は、内部の均一な磁束をそのまま反映した配置となり、反磁界(点線矢印)が均一になります。反磁界がやっかいなのは、図2-7にあるように、磁性体内部で磁束と反磁界が不均一な分布をすることですが、楕円の場合は均一な配置(図3-3では、実線が磁束、点線が反磁界)になる、と言う特長があります。このため、楕円体に限っては、反磁界係数の理論式(数値計算でなく)を作ることができます。この特長を利用して、一般の磁性体については、その形状に応じて楕円体に近似して反磁界係数を計算します。ちょっと荒っぽい近似ですが、真実の反磁界は、全体の形状以外に磁化の内部分布や表面の形にも依存するので、正確に求めるのは、細かい数値計算無しでは不可能です。そこでエイヤ!!と結構大胆な楕円近似をやってしまうわけです。この時の注意点ですが、磁性体は磁界の中で均一に磁化が進行するわけではないので、正確にはその時々の反磁界の分布があり、とても一個の定数で済ますことはできません。が、反磁界はとにかく計算が難しい。そこで磁気工学の世界では止むを得ず、この荒っぽい楕円近似が横行しています。とにかく他の方法よりも簡単なのです。どうやって近似するかは、(参考文献3-3)に詳しい説明がありますが、ここでは、面倒でないやり方を紹介します。
②特定形状の近似計算
反磁界は、磁性体に付いて回る問題ですから、古い概念にもかかわらず、時々、反磁界係数の計算法に関する論文が出てきます。大変にありがたいのですが、多くは計算が複雑すぎて使うのが面倒になる。その中から、実験にも使いやすいものを紹介します。なお、楕円体の反磁界係数の詳しい計算式は、(参考文献3-3)にあります。
Osbornの計算式(DemagnetizingFactors of the General Ellipsoid, J.A Osborn, Physical Review, Vol.67,No.11,pp.351 (1945))
楕円体の反磁界係数を基礎として、いろいろな形状に対する近似式を与えています。我々は、非常に幅の細い薄膜試料(幅10~100μm、厚さ1μm前後)の反磁界評価などに使ってました。
直方体、円筒状の近似式(Simple and approximate expressions of demagnetizing factors of uniformly magnetized rectangular rod andcylinder, M. Sato and Y.Ishii, J.Appl. Phys. 66, vol 2, 983 (1989))
形状が直方体と円筒に限られますが、楕円体による反磁界係数に近い値が得られる計算式の提案。どうやってその計算式に到達したか、詳しい説明がないのですが、非常に便利です。
最後に、反磁界係数の取り扱い方の例を挙げておきます。
図3-4は(a)ギャップの無いコア、(b)同じ材料で作った直方体の磁化曲線です。(a)は反磁界がないので、材料本来の磁化特性が測れます(測り方は、B-Hループトレーサーなど(第8章および参考文献3-4))。しかし、いつも(a)の形状の試料が手に入ることはないですから、反磁界係数を使って、(b)の磁化曲線から(a)を推定すると言う方法が採られます。 実際の実験室では、感度が高くて使いやすい磁気測定装置として、 VSM(試料振動型磁力計 第8章)が一般的ですが、その試料形状は(b)のようなものです。その測定結果から(a)の磁化曲線を得るには、以下のような「反磁界補正」を行います。
(a)では、
従って、(3-8)と(3-9)で同じ I にするには、Ha に代わって
Haは、外部から磁性体に加えた磁界です。I ( Ha ) とした理由は、μe が I ( Ha ) に対して定数でない( I が Ha に対して非線形に変化する、ほとんどそうなる)場合を考えているからです。(図3-1)に比べて、もっと現実に近い(a)のような磁化曲線を想定しているわけです。
(b)では、
の磁界が必要になり、(b)のように飽和しにくくなります。
「反磁界補正」は、試料の形から上記の近似で Nd を推定し、測定した磁化曲線(図3-1(b))から NdI を、さらに(3-10)を使って実験値の Ha' から Ha を求めて、試料本来の磁化曲線( I vs Ha )を再プロットする、というプロセスです。また、本来の磁化曲線がわかっている材料の素子設計には、素子の形状から Nd を決めて、Ha を Ha' に直して、と言う逆のプロセスを採ります。粗っぽい方法なので、精密な設計は電磁シミュレータに頼ることになりますが、シミュレーションの初期の段階で結果を見て頭を抱えた時には(大体そうなります)、反磁界が裏で効いてないか、この話を思い出してください。
なお、憶えておきたいことは、上記の反磁界補正の方法は、試料が常に均一に磁化していることを仮定していることです。弱い磁界中では、外部に磁束を漏らさないように磁区構造(第5章)ができるので、単純な補正では精度が落ちて来ます。
もう一度繰り返しますが、Nd は磁界を印加する方向によって変わります。図3-2のどれでもいいですが、I の方向が変わると、外部と内部の磁束の総量の比が変わるので、Nd も異なり、磁化曲線も異なります。これを「形状磁気異方性」といいます。楕円体の場合には、長軸(z)、単軸(x、y)のそれぞれの方向で計算式があるので(参考文献3-3)、ざっと眺めて反磁界と形状の感覚を掴んでください。
ところで、Nd = 1 になる形状があります。(2-21)で端部の磁極近くの Hd が I /(2μ0) であるので、両端部の磁極( N、S )が非常に近ければその2倍、つまり、
となった場合です。これは、(2-23)で、Nd=1とした時と同じです。このように磁極 N、S が極端に近づくのは、図3-2の(c)のような、薄膜(厚さ数ミクロン以下)の磁気モーメントが膜面に垂直に立っているときで、反磁界は(3-11)のように磁化の強さそのものになります。薄膜の磁性材料を膜面垂直に磁化するには、(3-11)以上の強い外部磁界か、磁性材料自身の強い「垂直磁気異方性」(あとで出てきます)が必要になります。
意外に知られていないことですが、強い垂直磁気異方性を持つ薄膜材料については、主に日米の多くの研究者が数10年に亘る艱難辛苦の末に、MD、ハードディスク(垂直磁気記録)に結びつけています。何気なく使っているPCのハードディスク、サーバーの中では、無数の磁気モーメントがGHzの速さで動いてます。ちょっと想像して見てください。また、その研究開発の歴史を反磁界というキーワードで見ると、「反磁界との闘い」であり、現在も終わっていないことがわかります。
さて元に戻って、上のような薄膜は、垂直方向には d = 1 ですが、これを z 方向として、他の方向(x、y)では Nd = 0 です。つまり、薄膜の面(x-y)内に I がある時は、端部の磁極は極くわずかで、外部磁束も少なくなり、実質的には反磁界はゼロです。この Nd の総和が 1 であることは、全ての形状で常に成り立っていて、
さらに、磁性体が球状であると、三方向の Nd は同じ筈ですから、
実効的な透磁率は、
μe が大きいときには、
となります。つまり、球状では形状磁気異方性は無いが、強い反磁界があり磁化曲線は寝ている、磁化しにくい、となります。磁性粉末は、球状に近い微粒子の集まりですが、がっちり固めないと透磁率が低くて使えません。一個一個の粒子が孤立していると、(3-13)の Nd が効いてくるからです。粒子の磁性については、「第7章 微粒子材料」、「補足Ⅲ 微粒子の透磁率」で、より詳しく議論してますので参照してください。
さらに、現実の実験室で生じやすい誤解の一例を挙げておきます。
図3-2(a)、図3-4(b)のような、反磁界係数の大きい素子を設計する場合に起こることですが、反磁界を考慮して実効的な透磁率を求めると、外部磁界の変化 ΔHe に対して、ΔI の変化があるとすると、
となり、実質的な透磁率は、反磁界係数 Nd、すなわち素子の形状で決まってしまいます。たとえば、(3-13)の球状磁性体の透磁率は、磁性体の μe が非常に高いものであっても、μeff = 3 となり,透磁率は大幅に劣化します。このように素子の形状によって透磁率が決まってしまうので、設計に反磁界の影響が考慮されていないと、透磁率の高い材料を使っても無駄になることがあります。
最後に反磁界係数を使って、材料の形状が透磁率にどれくらい影響するかを実感できる計算例をあげておきます。
図3-5は、μe = 1000 の矩形の材料の実効透磁率 μeff を楕円近似の Nd を使って、(3-16)で計算した結果で、素材の高い μe が全く生かせていないことがわかります。ただし、この計算は、材料が均一に磁化されていることが前提なので、実際の材料では、外部に磁束を漏らさない磁区構造ができて内部、特に中央部では反磁界が低下します。ですから、外部磁界がゼロまたは十分に低いと、磁区構造の動きにより中央部では高い透磁率になり、さらに外部磁界が高くなって磁化が均一になってくると外部に磁束が漏れてくるので、上記の計算に合ってくることになります。
以上、おおざっぱな考察でしたが、これ以上は実際に透磁率計測をやって見るか、このようなモデルを理解した上でシミュレーションをやるか、になります。
反磁界については、まだまだ書き足りないのですが、もう読みくたびれているでしょうから、次に行きます。
(反磁界については、更にわかりやすい説明を「補足Ⅳ も一度反磁界」で試みております。
ご参照ください。)
磁束密度 B は、
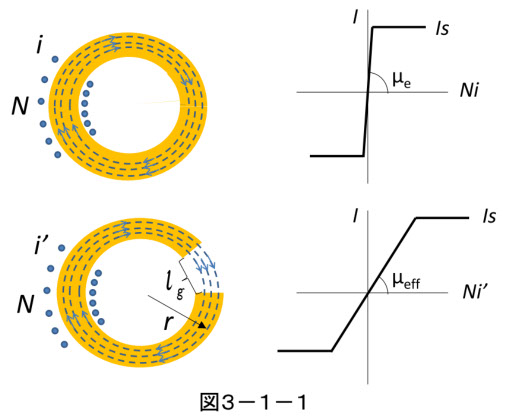
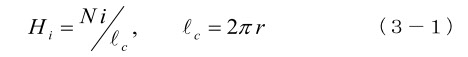
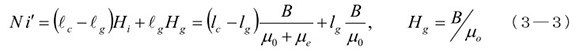
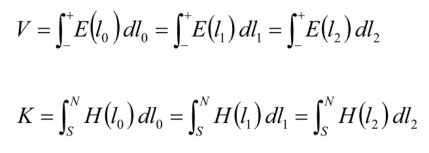
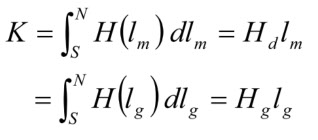

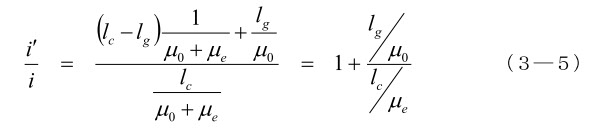
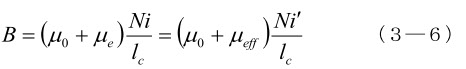
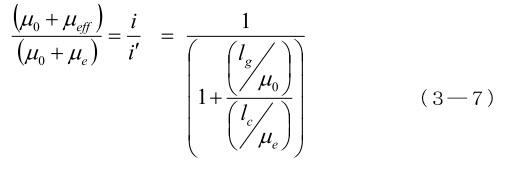
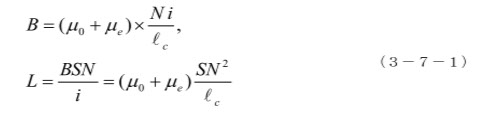
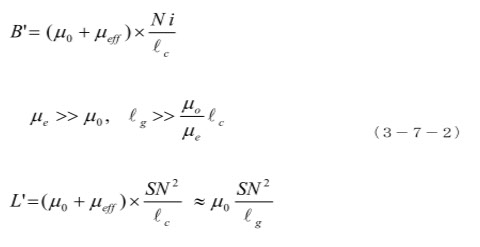
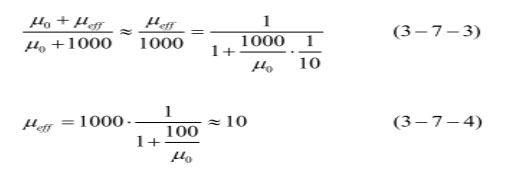
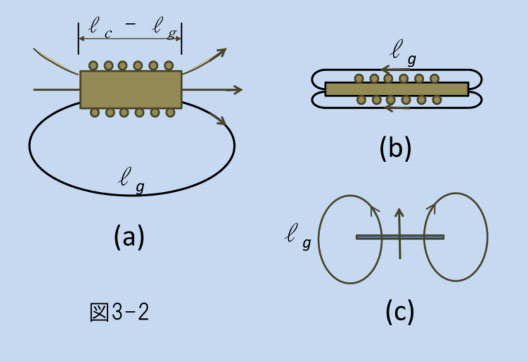
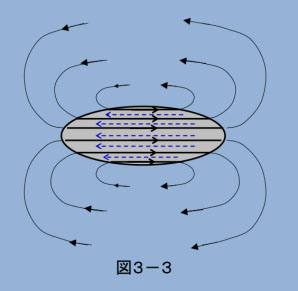
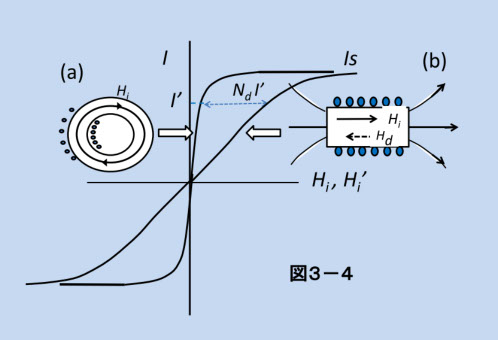

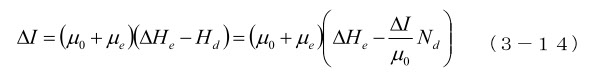
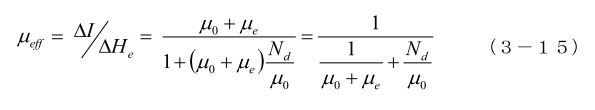
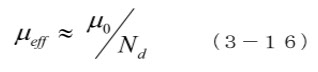
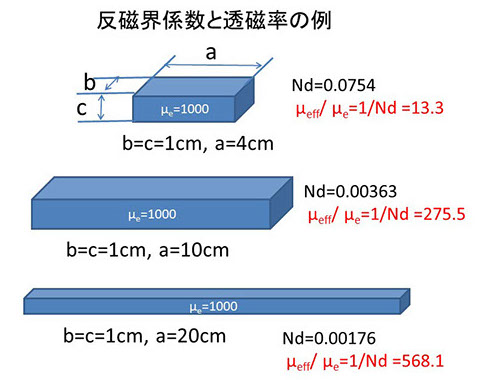
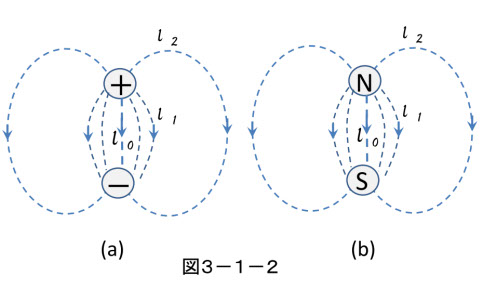
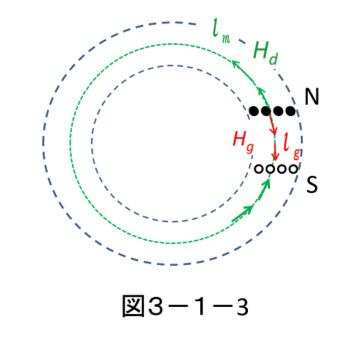
図 3-5
▲ページ上部へ