株式会社東栄 磁気応用部
サイトはこちら
磁気の話のはじめに
1.電荷と磁荷
2.磁気モーメントと磁性材料
3.反磁界と磁化特性
4.強磁性体
5.軟磁性材料
6.磁性材料と高周波
7.微粒子材料
8.磁気の計測
9.スピントロニクスについて
補足Ⅰ 多層膜の軟磁性
補足Ⅱ 薄膜インダクタ
補足Ⅲ 微粒子の透磁率
補足Ⅳ も一度反磁界
参考文献
磁性材料・磁気工学入門
© 2019 Yutaka Shimada

電磁気学の教科書や Web サイトの記事を見ると、電荷、電界、電束などについては、大変に詳しく解説されていて、理解しやすいのですが、磁荷、磁気モーメント、磁界、磁束、反磁界となると、一般にはとっつき難いのでは? 磁気物性、磁性材料の本をいろいろあたって見ると、このあたりは第一章で意外にさらりと触れていて、一応わかったつもりで勉強していくと、だんだんすっきりしなくなり、自分だけわかっていないような気がして不安になったりするものです。
このサイトでは、筆者が永年関わってきた「磁性材料、特に高透磁率材料の高周波領域での基礎と応用」あたりでうんちくを傾けたいと思っております。ですから、面倒な話は権威ある教科書の引用で済まして、さっさと先に行きたいのですが、どうも先にすすむにつれて引っかかりがでてきそうです。完璧にはできませんが、一応の解説を試みます。
1-1. 電荷と電子
電荷と磁荷はどう違うのか、を論じるには、まずは電荷とは?を考える必要があります。
電子は負の電荷(-1.602x10-19クーロン)を持っているので、電子がいれば負の電荷があることになりますが、正の電荷については陽電子が担っているわけではない。陽電子についての個人的な知識はごくわずかですが、数十年まえに読んだ真空に関する本の中に、宇宙創世(ビッグバン)期に大量の電子と陽電子が作られ、電子は原子核と結合して残ったが、陽電子は高速に拡散した、と書いてあったのを記憶しております。さて、この説は常識なのがどうか、うろ覚えなのでその本を探しましたが、どうしても見つからないので、このままにします。とにかく、陽電子は電子のようにこの世界に満ち溢れているわけではないのですが、現在の技術で陽電子を作ることは可能で、PET(ポジトロン断層法)や、陽電子消滅実験などで役立っています。
では、いろいろな話の中に出てくる正の電荷とは何なのか、簡単に言えば、物質の中の原子間の電気的結合や、金属中の電子と原子核内の陽子の正負電荷の分布のバランスがずれて、正の電荷が残る、と言えばいいと思います。要するにイオン、半導体の正孔、電界の中にある金属、等々です。
電界(E):
電荷 q によって生じる物理的な場。
その空間の誘電率に反比例するので、真空中では点電荷 q に対して、

電気力線とは、
電界の空間分布を表す線、その接線が電界の方向、その電界が強ければ電気力線の密度が高くなる。
電束密度(D)とは、
電気力線は、(1-1)でわかるように空間の誘電率に依存するので扱いにくい。そこで誘電率から独立した値として、電荷が単位電荷(1クーロン)であれば、一本の電束 D がある、と定義する。電束の総量は電荷 q になるので、D を電荷 q を囲む面で積分すると、

となり、微分形では、

となります。次には、この違いについて書きます。
ベクトル表現には、(1-2)、(1-3)、(1-4)のように、上線つき、または D, B と太字斜体にします。
1-2. 磁荷と円電流
中学生あたりの教科書では空芯コイルに直流電流を流した場合、N 極,S 極という磁荷(+m, ─m)が生じて、N から S へ向かって磁束が流れる、といったような説明があるのが普通です。しかし、上の式(1-4)では N も S も無い、どこでも常にゼロ、と言ってます。数10年前、著者が学生の頃)の核融合技術が次世代のエネルギー源として盛んに開発研究されていた頃ですが、超高密度のプラズマを真空容器内の空間に十分な時間だけ閉じ込めて融合反応を起こすためには、磁場の袋をつくればよい。と言うので非常にたくさんの形の磁界分布と磁界中プラズマの不安定性(plasma instability)を論じた論文が発表され、筆者もプラズマの勉強をしていたので、難しい理論に悩まされました。しかし、現実は、どうしても磁界の袋の端を閉じることができないので、プラズマがもれだしてしまう。やっぱりN、S の磁極で袋の端の穴を閉じる必要がある、と言うので本気で単磁極の探索をした研究者もいましたが、結局無駄な努力でした。現在の磁気の世界では、電子の電荷に相当するものは無い、と言うことになります。これを表している上の(1-4)式は、B の連続性を表し、(1-3)とともに電磁気学の基本法則である Maxwell の式の一つです。実際、単独の磁極が見つかれば物理、工学の基本法則の一つがひっくり返り、ノーベル賞確実、と言われています。
その後、核融合開発におけるこの instability 問題はどうなったのか、実は全く無知ですが、単磁極が見つかったという話は勿論ないので、(1-4)は厳然として物理の世界を支配しております。
でも、磁気の世界では中学生の理科のように、N、S と言う磁荷を仮想的にあるものとすると、磁界の分布計算などが容易になり、また真実に近い結果が得られます。そうなると、「ここに磁荷があると仮定」して、あーだ、こーだとやっているうちに、磁荷があるのが当然のような議論が始まる。実際、磁気に関する多くの教科書の入り口ページあたりに、「磁荷」、「磁極」が突然現れます。これでは真面目な学生の頭が混乱することもありそうです。本稿でも、いろいろな場面で仮想的な N、S を使うことがありますが、まずは、この混乱をできるだけ排除すべく、話をすすめます。
図1—1 は、磁気の解説記事に必ず出てくる空芯コイルです。図のようにコイル巻き線に直流電流を流すと、磁界 H が発生します。(物理の世界では“磁場”です。どっちでもいいですが、以降はだんだん工学的になるので“磁界”とします)。磁界は、電界、重力場と同じく、空間に存在する場のひとつです。真空(コイルは空気中にあるはずなので、窒素、酸素、水の影響がありますが、面倒なので真空中にあると考えます)には、透磁率 μ0 がありますので、磁界によって磁束 B = μ0Hができます。B は磁束密度(単位面積を通過する磁束の本数)で、電界 E に対する電束 D と似た関係にあります。
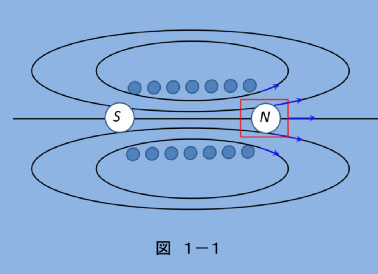
しかし、この B には、(1—4)式が適用されます。図1-1 のどこでもいいですが、特に、N 、S があるとされているコイルの端のあたりに、単位体積の立方体を考えます。図では二次元(赤線)で書いています。この立方体の中に単独の磁荷 N があれば、立方体に入っていく磁束と出ていく磁束の数に差があるはずですが、(1-4)式の意味は、この立方体に入り込む磁束の本数と出て行く磁束の本数は常に同じ、ということです。磁束の増減が無い、と言うことは、N 、S は無い、ということで、(1—4)式は図1—1 の空間のどこでも成り立っています。
(1—1)、(1—2)式の電場、電束は、まずは電荷があり、そこから E 、D を算出すればよかったのですが、磁界、磁束は、まずは電流による磁界 H を算出し、それから空間の透磁率を使って磁束密度B を算出することになり、磁界、磁束の取り扱いもすっきりした感じがします。
ならば、敢えて N 、S を仮定して B を求めたら何かいいことがあるのか?…あるんです。実は、ここに深い意味があります。以下にこれを説明します。
図1—2には、(a)にコイル内外の磁束分布、(b)にはコイル端に N 、S を考えたときの磁束分布を描いています。何の計算もしてないので、相当にいい加減ですが、両方を比べると、コイル内部は、方向が逆で全然似ていません。一方、コイルの外部の磁束分布はよく似ています。お前が似るように描いたんだから当たり前だ、と言われそうですが、実際、N 、S を適切に配置すれば、いろいろな磁束分布計算に使えるくらいに似ているんです。

この似ていることをもっと突っ込んで考えます。磁気物理、磁気工学で厳密な物理量として扱えるくらいに、この二つの分布が同じ、と言えるのはどんな状況か、を考えると、以下の二つがあります。
①コイルを非常に遠くから眺めて、眺めている位置付近の磁束分布を計算した場合
②我々が取り扱う材料、計測技術の実験室スケールに比べてコイルのサイズが
非常に小さい場合
の二つです。前者はあまり使い道がないので、後の小サイズのコイルを考えて見ます。
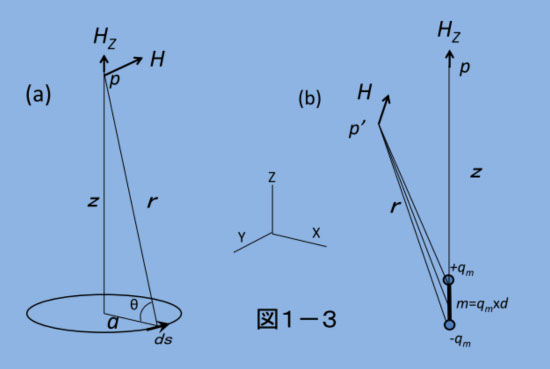
図1—3(a)は、小さなコイル(図ではコイルでなく1ターンループ、大きく書いてあります)から十分に離れた位置 p での磁界強度の計算モデルです。(b)は、コイルの代わりに、磁荷 +qm、-qm を距離 d だけ離して置き、コイルを磁極に置き換えたモデルです(qm × d = m を磁気モーメントの強さと言います。)。(b)では、図面の分かりやすさの都合上、磁極から r 離れた点 p' での H を示しております。さて、この図を比較する目的は、r が十分大きい場合に、小さな1ターンコイルの電流による磁界と微小な磁気モーメントによる磁界が同じになる条件、つまり、1ターンコイル電流が等価的な磁気モーメントと見なせる関係式を求めることです。なぜそんな作業が必要か、ですが、実は、電子が原子核周りの軌道上で運動している場合、ミクロなコイル電流と見なせるからです。各軌道の電子が作るコイル電流を磁気モーメントの大きさに置き換えると、磁性材料の磁気の根源はミクロなコイル電流による磁気モーメントの集合体である、というイメージになり、単位体積あたり磁気モーメントの基本量(Bohr magneton、あとで出てきます)の何倍、つまりこの材料の「磁化の強さ」は磁気モーメントの量を使ってこれこれ、と表現できます。いちいち軌道電流の大きさ、半径と数は?そこからの磁界は?などとやっているよりもずっと楽になるのです。
厳密にこの関係式を作るには、図の a << r になる全ての点で成り立つことを証明しなければなりませんが、面倒なので p 点の磁界 Hz を比較して関係式を作ります。その関係式は、図の a << r になる全ての場所で成り立ちます。
まず、(a)の p での磁界強度は、ビオ・サバールの式から(参考文献1-4)、

dH は、ループ電流の素片 ids による磁界で、Z 方向のベクトル成分 Hz は
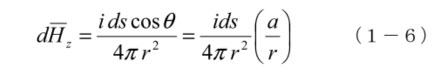
ds の積分値は 2πa であるから、ループ全体からの磁界 Hz は、
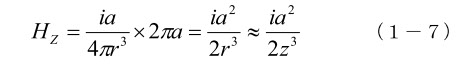
p 点では X,、Y 方向の磁界成分は対称的に分布して総和はゼロになるので、Hz のみが残ります。
次は(b)です。磁気モーメント m が作る磁界については、便利な式がありますので(参考文献1-5)、それを使います。磁気モーメント m による p’ 点の磁界 H は、
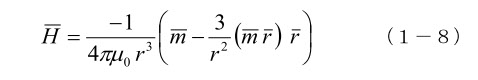
この式を使うと、単独で存在する磁気モーメント周辺の磁界分布を正確に求めることができます。
今は、p’ は p の位置にあるので r = z、 (1-8)から
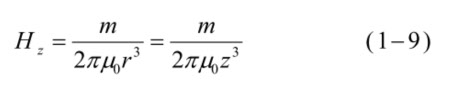
(1-7)と(1-9)が同じになるには、
‾n : ループ面に垂直なunit vector
つまり、面積 S(= 2πa2)のループ電流 i による磁界分布は、(1-10)式で表される磁気モーメント m が作る磁界と同じ、ということです。ここまで来ると、磁荷 qm と距離 d の大きさ、コイルの r などは忘れてしまって、「ミクロな円電流は磁気モーメント m に置き換えることができる」という事になります。この磁気モーメントは、N、S 極を仮定したモデルですから、いくら探しても見つかるものではありませんが、円電流を等価的な磁気モーメントに置き換えて、Bohr magnetonを単位として数えることで、磁気物理、磁気工学が出来上がっている、ということです。
この原子レベルの磁気モーメントの基本量である Bohr magneton は、なぜ必要か、ですが、電子の軌道は量子化されているので、とびとびの値しか取れない、で、磁気モーメントも量子化した基本量(Bohr magneton)が必要になります。
1-3. 軌道磁気モーメントとスピン磁気モーメント
Fe、Ni Co は、室温でも強磁性を示します。強磁性については第4章で詳しく説明することにして、ここでは、そもそも「磁性を示す」とは何か、を簡単に説明します。それぞれの原子核の周りの電子がもつ磁気モーメントで、その基本単位は、上記の Bohr magneton ですが、実は、電子の持つ磁気モーメントには、「電子の軌道運動による磁気モーメント」に加えて電子自身が持つ「スピン磁気モーメント」があります。前者は、これまで説明したようなループ電流のイメージで理解できます。が、後者のスピン磁気モーメントは、説明が難しいです。荷電粒子である電子自身のスピン(コマと同様な回転運動)によって、スピン磁気モーメントが生じている、と言う解釈が最も妥当に見えます。しかし、実験で計測されるスピン磁気モーメントの大きさは、古典的なコマ運動(電子を適当な体積の球として、光速に近い速度で回転させる)から計算した円電流による磁気モーメントよりもはるかに大きく、スピン磁気モーメントは古典電磁気学的イメージではありません。素人的には、「量子論的な仮説が立てられ、実験と理論によって実証された電子固有の磁気モーメント」、として受け入れることになります。図1-4は、電子軌道に乗っている電子のループ電流による磁気モーメントとスピン磁気モーメントのモデル図です。後程説明しますが、一個の電子軌道には、2個の電子が乗っていて、スピン磁気モーメントは互いに逆方向になっているので、各軌道でのスピン磁気モーメントはゼロになっているのが普通ですが、磁性体(常磁性体、強磁性体、フェリ磁性体、反強磁性体その他)では、電子が単独で居る電子軌道があって、スピン磁気モーメントが外部から観測できるのです。
以上は物性物理的にはあまり正確ではありませんが、当面は、そんな説明で話をすすめます。
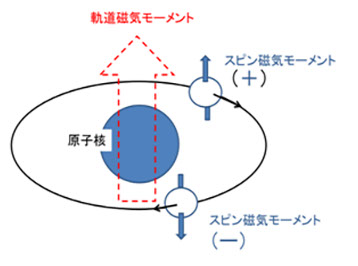
図1-4
実際、上記の強磁性体の金属では、結晶格子からの対称性の高い電場に曝されて、電子の動き(軌道)が格子の対称性に沿った形で拘束されています(軌道の縮退が解ける、といいます)。この時には、ループ電流を作る確率が少なく軌道角運動量は非常に小さくなり、むしろスピン磁気モーメントの方が幅を効かしています。最近の磁気工学の分野で大流行の「スピントロニクス」(第9章参照)のスピンは、このスピン磁気モーメントのことで、主役になっていることでも、その重要さがわかります。スピン磁気モーメントについては、第2章、第9章で詳しく説明します。
ちょっと脱線気味ですが、上記以外の磁性体で有名なのが、希土類金属(レアアースメタル)です。レアアースメタルの幾つかは、大きな軌道磁気モーメントを持っていて、しかも、その電子軌道( 4f 軌道)は、もっと大きい(外側にある)電子軌道群( 5s、5p、6s )にマスクされています。このため、結晶格子の電界はシールドされて、軌道磁気モーメントとスピン磁気モーメントが両方生き残っていています(参考文献1-6)。さらに外側の遍歴電子(原子から原子へ移動できる外殻電子)を通した磁気的結合(RKKY理論)(参考文献1-7)によって、Fe などのスピン磁気モーメントとの相互作用も強く、結果として遷移金属-希土類金属の合金のいくつかは非常に強い永久磁石材料になります。この材料は、ハイブリッド車やEVに使われる高性能モーターの回転子のコアを始めとして、非常に多くの分野に応用が広がっています。例の尖閣諸島問題に関連して、中国が輸出を抑えたと言われている、超有名「レアアース」は、この希土類のことです。
▲ページ上部へ
