株式会社東栄科学産業
磁気応用部サイトはこちら
磁気の話のはじめに
1.電荷と磁荷
2.磁気モーメントと磁性材料
3.反磁界と磁化特性
4.強磁性体
5.軟磁性材料
6.磁性材料と高周波
7.微粒子材料
8.磁気の計測
9.スピントロニクスについて
補足Ⅰ 多層膜の軟磁性
補足Ⅱ 薄膜インダクタ
補足Ⅲ 微粒子の透磁率
補足Ⅳ も一度反磁界
参考文献
磁性材料・磁気工学入門
© 2019 Yutaka Shimada

6-1. バルク軟磁性材料の動的損失
バルク磁性材料の動的損失とは、たとえばアモルファス薄帯のように、図5-6のような磁壁の高速移動による渦電流、また、図5-8のような磁化回転による渦電流によって起こる熱損失を言います。また、5-1で触れた、静的な磁化反転でも起きるヒステリシス損失もありますが、これは周波数に比例して増えるのに対し、渦電流損失は指数関数的に増えるので、ずっと大きい損失になります。
バルク材料(たとえば電磁鋼板)のほとんどは、大振幅磁化反転で使うので、励磁電流が増えるのを嫌います。そこで、励磁電流が少なくて済む(B-Hカーブの立ちあがりのよい)容易軸方向の磁壁移動での磁化反転を使うことになるので、バルク材料の損失は、図5-6をモデル化して考察します。図6-1は、そのモデルです。図では、外部磁界 He が奥に向いていて、時間とともに増えつつあり、磁壁はHe と反対方向の磁区( -I )が狭くなる方向に動いています。この後、He は最大値に達する と減少に転じ、ゼロになって反対方向に増えていきます。この He の変化は、通常は低周波(50~数10KHz)のsine波形になります。単位体積当たりの平均磁化 ΔI は、振幅のピーク値( Im )になると反転してゼロを通過して -Im になるまで増えていきます。この時の磁壁運動によって発生する渦電流からJourle損失を計算したのが、(6-1)式です(参考文献6-1)。
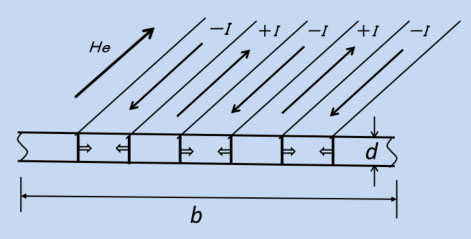
図6-1
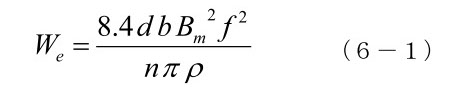
n : 試料幅b の内にある磁壁の数
なお、(6-1)では、Im の代わりに Bm になっていて正確ではありませんが、これは原典に従っています。いずれにしても、He は軟磁性材料の磁壁移動の駆動磁界なので磁化回転の駆動磁界ほど強くない、μ0He は無視しても問題ないでしょう。
(6-1)の意味は、磁壁移動による渦電流損失は、磁束の振幅 Bm、駆動周波数 f の二乗に比例、電気抵抗 ρ に反比例し、また、磁壁の数 n が多ければ、損失は少なくなります。これは、単位長あたりの磁束の変化(Bm~-Bm)を担う磁壁の数が多いと、一枚の磁壁の移動距離と移動速度が小さいので、渦電流も減るためです。図5-3(a) の Fe-Si の磁区を細かくしているのは、このためです。
(6-1)の関係については、詳しい検証実験が行われています(参考文献6-2)。いろいろな軟磁性材料(結晶性、アモルファスの薄帯(薄板状)磁心)の渦電流損失の周波数依存性を測定すると、Bm、 f の二乗に比例するのではなく、各材料について、We ∞ Bmxfy、(x, y < 2)となり、その原因は、磁壁の数 n が、それぞれの材料と周波数によって変わり、一定でないためであることがわかっています。つまり、実験で n の周波数依存性を測定し、(6-1)に適用すると、n × We ∞ Bm2×f2が各材料で成り立っていて、(6-1)は n の周波数変化を考慮すれば実験値を記述することになります。静的な動きでは、磁壁の数 nはそれぞれの材料で異なっていて、周波数が上昇するか、または磁束の振幅が大きくなると、急激に増えていきますが、ある限界値 nmax に達すると、後は周波数について行けなくなり、磁壁の移動速度が上がって損失が増すばかり、となります。
ここで、We の検証実験の詳細(参考文献6-2)を見せるべきところですが、ちょっと複雑な図なので、ここでは、適当に抜粋したものを図6-2に示します。厚さ数10~数100μm の板状パーマロイ、アモルファス薄帯などの渦電流損失の周波数依存性です。この時の磁束密度の振幅 Bm は一定(0.3 Tesla)にしています。各材料の周波数依存性は異なっていて、その理由は上に述べたように、(6-1)の n が周波数に対して、異なる変化(増大)をしているからです。 渦電流損失は、周波数に対して指数関数的に増えるので、実験した周波数上限は、約100KHzになってます。このような損失の急激な増大は避けたいので、大振幅の磁壁移動を利用する磁気工学は、もっと低い周波数(最高で数10KHzくらい)の話になります。高周波大振幅の需要はないのか、と言うと、最近は、電気自動車(EV)のモーターの高性能化(高速回転、高出力)など、何かと騒がしくなっていて、5-2-2で触れたような、高速・大振幅磁化反転でも渦電流の心配が少ない粉末磁心が見直されています。
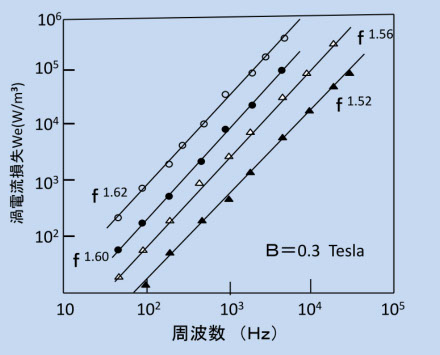
図6-2
では図5-8の困難軸方向の磁化回転はどうか、ですが、異方性磁界に打ち勝って磁化を増やす必要があるので、励磁電流が増えてしまって大振幅では使えません。磁性材料の磁化回転を利用するのは、小振幅の使い方、つまり、電力機器でなく高周波の信号処理、伝送機能を持つ通信機器などの場合で、渦電流損失の大きさよりも、小振幅の透磁率が高周波でどのように劣化するか、が重要です。(6-2)は、小振幅の磁化回転(小振幅透磁率)の時の透磁率の式です(参考文献6-1)。計算のモデルは、図5-8と同じですが、図6-1との対比のために、図6-3に再現しておきます。磁壁と磁区は、図のx方向にできているはずですが、省略しています。図6-3では、磁気モーメントM (単位体積では磁化 Is )が困難軸方向の高周波磁界 He( RF )によって微小な振動をします(実際は、歳差運動ですが、ここでは振動とします)。これによって、He( RF )と同じy方向に、同じ周波数の磁化の変化(磁束の変化)ΔM が起きるので、図にあるような渦電流ができます。渦電流は、ΔM の時間的変化を打ち消す方向に流れます。
図6-3
この時の ΔM 方向の静的な透磁率は、μha = Is/Hkです。磁気共鳴のことは忘れて渦電流の効果だけを見るために、μha は周波数に対して一定とし、μdcとします。渦電流は、試料幅が試料厚み d に対して十分大きいと、図6-3のような電流分布になり、端部を無視すれば、図6-4のようなモデルで電磁気学の理論計算ができます。
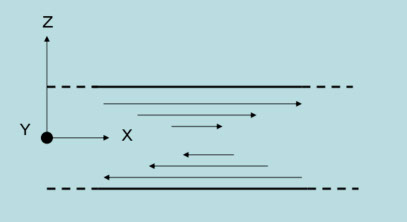
図6-4
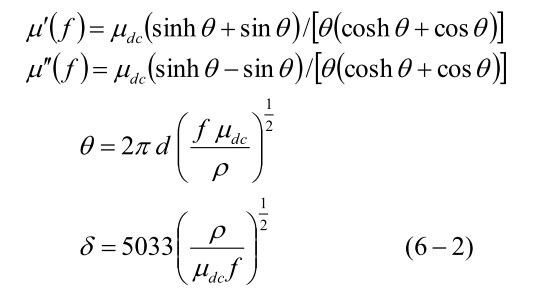
渦電流は、図6-3のように外部磁界を打ち消すように流れるので、内部の磁界が弱くなり磁束の変化量も減るので、外部磁界から見た実効的な透磁率も内部では小さくなります。これを試料厚みdで平均した値が(6-2)のμ’(f)、μ”(f)です。また、外部磁界の変化に対応して内部に電流が流れるわけですから、抵抗損失(熱損失)があります。(6-2)の μ”(f)は、その等価的な抵抗分に相当します。つまり、μ’(f)はインダクタンス、μ”(f)は渦電流によって現れた抵抗になります。電気回路の式では、
μ( f )=μ'( f )-jμ"( f ) (6-3)
となり、μ”(f)は、位相が90°遅れた分、つまり抵抗分を表しています。このμ(f)を使って、磁性体に巻線をしたインダクタンスを計算すれば、L - j R となります。一方、Rの方を位相ゼロの基準とすれば、R + j Lで、一般に使われる電気回路の式になります。つまり、(6-3)は、インダクタンスを基準(ゼロ位相)として表していることがわかります。
(6-2)の δ は、表皮の深さ(skin depth)で、図6-3の電流が表面の電流から1/e(e=2.718)になる深さ(z)を表し、工学的には、これ以上厚くしても熱損失が出るだけで無駄、となる厚さの限界を判断することに使います。なお、(6-2)は、電磁単位(emu)で表しています。一方、δの式だけは、計算しやすいように、ρ は Ωcm 、μは emu ( μ0=1 )を入れると cm で出てくるようになっています。
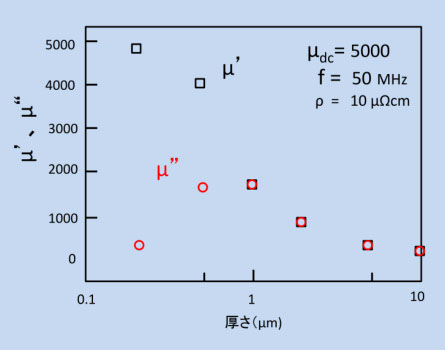
図6-5
図6-5は、(6-2)を使って、仮想的な材料(パーマロイ的)のμ'、μ"を計算したもので( emu に換算する。例えば、10μΩcm ⇒ 10×10-6×109 emu を使う)、この材料を50MHzで渦電流損失なしで使うには、約0.2μm 以下に薄くする必要があります。この時は、δ=0.3μm になります。1μm以上では、μ' = μ" に近づきますが、μ' < μ" にはならない。これは、渦電流はμ'の大きさで決まって、μ" はその結果であるからです。
以上の話をまとめると、
- 磁壁移動による磁化過程では、低い励磁電流で大振幅磁化反転ができるが、磁壁移動は渦電流損失を伴うので、低損失のためには磁壁の数を増やすことが有効である。低周波での電力変換(変圧器、モーターなど)に利用される。
- 磁化回転による磁化過程は、小振幅の透磁率を使う高周波信号処理、伝送技術に利用される。渦電流を低減するには、δを参考にして厚みを制限(薄膜状に)する。渦電流を無視できれば、磁気共鳴周波数まで一定の透磁率を維持できる。
6-2. 薄膜の透磁率
前節で、試料を薄膜にして磁化回転を利用すると、高い周波数まで磁性材料の利用が可能になる話をしました。その周波数上限は磁気共鳴ですが、磁気共鳴そのもの、さらに磁気共鳴周波数以上の領域を工学的に利用する研究も多くなっています。また、薄膜と言えども、非常に高い周波数では渦電流が無視できなくなります。ここでは、薄膜の磁化回転(小振幅、困難軸方向)による透磁率の高周波特性を詳しく説明します。
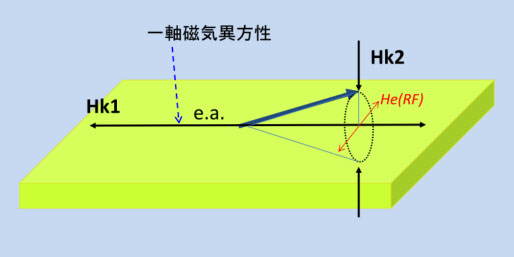
図6-6
図6-6は、薄膜特有の磁気モーメントの動作を表しています。
まずはお断りです。飽和磁化 Is は、単位体積あたりの磁気モーメント M の数に相当し、これは、SI単位ですが、ここからは、emu 単位になります。理由は、原典が emu なので、SI 単位に直すと間違いが怖いからです。emu単位では、磁化の強さはM、飽和磁化は Ms(emu/cm3)、磁束密度は 4πMs (Gauss)です。単位換算表は、いろいろな教科書やWebにあります。
図6-6は、図5-8、および図6-3と同じく、高周波磁界 He( RF )中の薄膜の磁気モーメントの動作を示していますが、歳差運動を入れてもっと正確な動作を表しています。図2-2は、磁気モーメントの歳差運動を説明していますが、それによると、歳差運動のために磁気モーメントは、図6-6のように、膜面から立ち上った時間帯があります。膜面から立ち上がると、磁気モーメントには膜面に垂直なベクトル成分ができるので、形状異方性磁界 Hk2(膜面内を容易面とする)が働き、磁気モーメントを膜面内に抑え込もうとします。
このように、薄膜の磁気モーメントは二つの磁気異方性の影響下にあり、一つは誘導磁気異方性(面内の一軸磁気異方性)の Hk1、もう一つは面垂直方向が困難軸となる形状磁気異方性 Hk2 です。この二つを考慮して、薄膜の透磁率を計算します(参考文献6-3)。ちょっと長くなりますが、なるべく簡単に説明します。
第2章に戻って、図2-2は、磁気モーメント M の歳差運動を表しています。ここでは、この M は、単位体積あたりの磁気モーメントの密度とします。図2-2の運動を式で表すと、
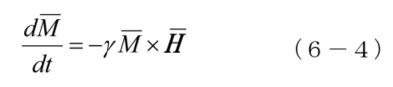
となります。図6-7にその関係が示してあります。図中の MxH は、M が磁界 H から感じる回転力で歳差運動の原因となり、右辺は、磁気モーメントの角運動量の時間変化に対応する力で、(6-4)は、この両者が等しい、と言っているわけです。その間をつなぐのが、ジャイロ磁気係数 γ(磁気モーメントと角運動量の比)です。
この歳差運動は、材料中では格子振動などによる損失のために、その振幅が減衰していくので、これを式に入れるために、図6-7のように H の方向に向かうような力が働くと考えます。これを現象的に式で表すと、
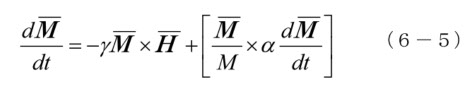
右辺第2項の αdM/dt は、歳差運動が受ける制動力を表していて、その制動を受けた結果は、( M/M)× αdM / dt、すなわち中心方向を向いた力になっていることを表しています。α は、磁気モーメントの歳差運動のブレーキになるすべての損失を含む、とする現象論的な定数で、各材料に固有の値になります。普通は α <<1であるので、(6-5)の右辺( dM / dt )を左辺に代入すると、以下のLandau-Lifshitz-Gilbertの式(L- L式)になります。この式のほうが、(6-5)よりも解析が楽になります。

この式は、磁界の影響下での磁気モーメントの運動を表す基本式です。この右辺で表される力の方向が図6-7の矢印(点線)です。
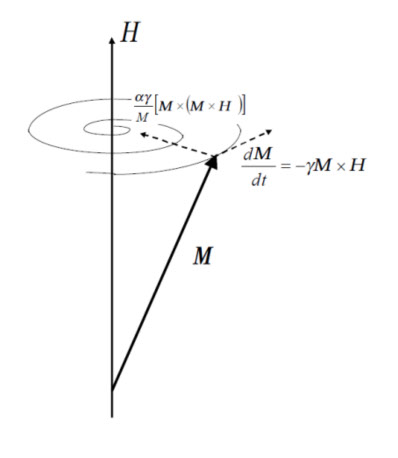
図6-7
図6-6の薄膜の磁気モーメントは、Hk1(誘導磁気異方性:面内)、Hk2(反磁界:面垂直)の影響下にあり、さらに微弱な高周波磁界 He( RF )を考慮して、LL 式を解析することになります。そのプロセスは、かなり長いので、(参考文献6-4)に任せることにして、結果だけを示します。
まず、高周波での透磁率は、非常に弱い高周波磁場 He( RF )によって駆動される磁気モーメントの動きですから、初透磁率 μi とします。(一般的な初透磁率とは、微弱磁界中でB-Hループのゼロ点から磁化が動き始める時の透磁率を言います)
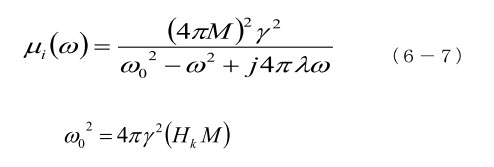
ω0は、共鳴角速度(=2πfr )、Hk は、一軸誘導磁気異方性磁界、λ=αγM
ω0が、(2-11)のωLと異なるのは、単一の Hk ではなく、二つの Hk(誘導磁気異方性と反磁界)があることで、そのために、誘導磁気異方性の Hk と、膜面垂直の反磁界( emu単位では4πM )によるMが入っていることです。(式中の4πは、単位の違いによるものです。)
これで、(6-7)を実数と虚数に分解すれば、透磁率 μ’と μ” の周波数特性が出るはずですが、実は、(6-2)の渦電流による透磁率への影響を考慮する必要があります。(6-2)と(6-7)を組み合わせると、
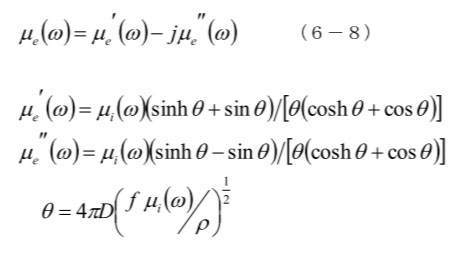
μi (ω) は(6-7)の薄膜の磁気共鳴、またμe(ω)は、さらに渦電流も考慮した初透磁率になります。いろいろな薄膜材料の透磁率は、それぞれの飽和磁化( Ms )、誘導磁気異方性 Hk1 、膜厚 D、抵抗率 ρ を使うと、(6-8)で計算できます。この理論式の特徴は、透磁率測定の実験結果と良く一致することで、将来に開発したい材料を仮定して、その周波数特性を予測することもできます。ただし、材料の反磁界は、膜面に垂直であることを前提にしているので、非常に細かい薄膜パターンでは、Hk2(面垂直方向の異方性磁界)が 4πMs にならないので、もう一歩踏み込んだ計算が必要です。つまり、「膜厚に対して膜面積が十分大きい場合によく一致する」ということです。
この縦、横、高さが多様な材料の計算には、それぞれの方向の反磁界係数がわかれば、「Kittelの式」(参考文献6-5)が使えます。また、その他の異方性磁界についても計算があります。ただし、磁気共鳴周波数の計算だけです。
では、(6-8)を使って、薄膜材料の透磁率を計算してみます。
以下は、代表的な薄膜材料の飽和磁化、Hk(誘導磁気異方性)、抵抗率です。(emu単位です。)
飽和磁化(4πMs)
Hk
ρ
Ni80Fe20
(結晶、パーマロイ)
10500
(Gauss)
3
(Oe)
50
(μΩcm)
〜50
(μΩcm)
Fe74Si16.5Al9.5
(結晶、センダスト)
10000
(Gauss)
──────
150
(μΩcm)
Co85Zr5Nb10
(アモルファス)
10000
(Gauss)
16
(Oe)
100
(μΩcm)
Co76Ta6C10
(ナノクリスタル)
14000
(Gauss)
15
(Oe)
1100
(μΩcm)
Co56Al10O34
(グラニュラー)
9000
(Gauss)
80
(Oe)
以上の内、センダストは5-1節で説明したように、誘導磁気異方性がほぼゼロなので、磁化回転と磁壁移動が混在し、上記の理論に乗りません。パーマロイの抵抗率50μmは、文献の抵抗率(15μm)より高いですが、薄膜では不純物や格子欠陥、空隙の密度が高いので、これ位になる、という値を仮定しています。また、5-2-5-bで説明したグラニュラー膜は、Hk 、ρが大きく、異色の材料です。
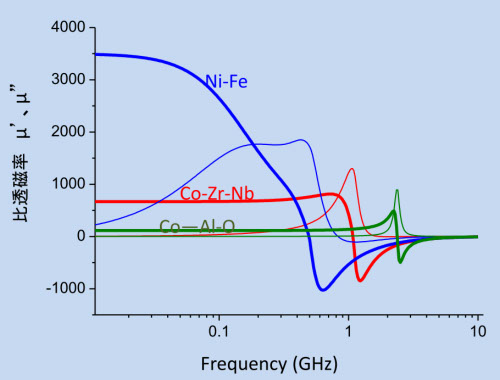
図6-8
図6-8は、膜厚 1μm を仮定した(6-8)の計算結果です。太線が μe’ 、細線が μe” です。パーマロイは、Hkが小さいので、透磁率が非常に高いですが、その分、渦電流も大きくなり、100MHz付近から μ’ が低下し、μ” が増えてきます。また、磁気共周波数は約500MHzですが、その変化は、ほとんど渦電流に埋もれています。Co-Zr-Nbは、Hk がパーマロイの約5倍、電気抵抗も3倍くらいあるので、透磁率は低下しますが、渦電流の影響はほとんど見えません。Co-Al-Oは、Hk、電気抵抗ともに非常に大きいので、透磁率は100程度ですが、2GHzくらいまで一定です。GHz帯まで透磁率が100を保っている材料は、グラニュラー薄膜以外には見たことがないのですが、これは、グラニュラー構造は、薄膜でしか作れないのが残念な点です。しかし、あまり厚くなると、やはり電気抵抗が十分高くないことがわかります。図6-9は、Co-Al-Oの厚みを増やした時の計算です。5μmでは問題ないのですが、50μmになると、渦電流に負けて、この周波数帯(1MHz以上)では利用価値がなくなることを意味しています。このことは、高周波では磁性材料の渦電流の影響は非常に大きく、電気抵抗を2、3桁増やしたくらいでは間に合わないことを示しています。
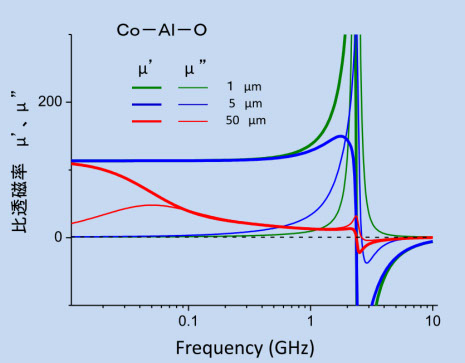
図6-9
しかし、電力変換器(トランスなど)の低周波動作(磁壁移動による磁化反転)では、(6-1)でわかるように、ρの数桁の増大は渦電流損失の低減に劇的な効果が期待できます。バルクのグラニュラー構造は研究課題として魅力的ですが、今の処は夢の材料でしかありません。
薄膜の高周波特性についての詳しい解説が以下にあります。
島田:連載講座 軟磁性材料 薄膜Ⅲ「薄膜の高周波特性」 日本磁気学会
「 まぐね」 (Magnetics Japan)4(2), 93-100, 2009
ここでは、薄膜の透磁率についての基礎の話がほとんどでしたが、磁性薄膜には、いろいろな使い方があり、いまでも進歩が続いています。
6-3. Snoek(スニーク)の限界
ちょっと話が前後してしまいますが、高透磁率材料の周波数特性の話で、「Snoekの限界」に触れないでいるのは、不見識に思いますので、以下、説明しておきます。( SI 単位に戻ります)
一軸の異方性磁界 Hk があるときの磁気共鳴周波数は、(2-11)から、
このときの透磁率は、(4-6)から、

この二つの関係から、

(6-11)を見ると、透磁率μを高くすると、磁気共鳴周波数frが低くなることがわかります。その積は、飽和磁化の大きさで決まり、これをSnoekの限界と呼び、磁性材料の高周波機能性の限界を示すものと見られています。Snoekは、Mn-Zn フェライトの組成を調節して結晶磁気異方性の強さを変えて、初透磁率の周波数特性を調べて、この限界を明瞭に示しています。(参考文献6-6)
この実験結果は、第7章でもう一度紹介します。しかし、この限界は、薄膜の場合にはもっと広がります。6-2節で話したように、薄膜では磁化を薄膜面内に抑え込む強い形状磁気異方性があり、その磁気共鳴周波数は、(6-7)から、
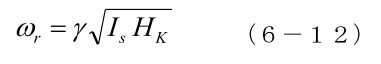
となります。飽和磁化 Is が入るのは、形状磁気異方性の反磁界が、薄膜では面に垂直方向に

であるからです。 この(6-10)、(6-12)から、
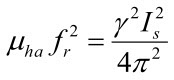
または
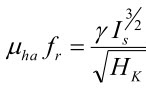
これは、「修正したSnoekの限界」とも言うべきもので、薄膜に一軸磁気異方性と形状磁気異方性があることが原因です。つまり、薄膜の透磁率も(6-10)で決まるが、(6-12)を見ると、fr は(6-9)よりも高くなり、薄膜の透磁率はより高い周波数まで一定であり、その機能性が広がることを示しています。ただ、注意しなければならないことは、形状磁気異方性は、その形状によって変わることで、例えば、薄膜のパターンが細線で、その幅と厚さが同じくらいになると、今度は細線の軸方向に強い一軸の容易軸ができることになり、もとの一軸磁気異方性も考慮して、どの方向に高周波励起をするかで透磁率、磁気共鳴周波数が異なることになります。
▲ページ上部へ