株式会社東栄 磁気応用部
サイトはこちら
磁気の話のはじめに
1.電荷と磁荷
2.磁気モーメントと磁性材料
3.反磁界と磁化特性
4.強磁性体
5.軟磁性材料
6.磁性材料と高周波
7.微粒子材料
8.磁気の計測
9.スピントロニクスについて
補足Ⅰ 多層膜の軟磁性
補足Ⅱ 薄膜インダクタ
補足Ⅲ 微粒子の透磁率
補足Ⅳ も一度反磁界
参考文献
磁性材料・磁気工学入門
© 2019 Yutaka Shimada

強磁性薄膜を中間に強磁性でない膜(Cu、Agなどの金属膜、あるいは酸化膜、窒化膜などの絶縁膜)を入れて重ねたものを、一般に多層膜、積層膜と呼んでいます。このうち、金属膜を中間膜にしたものは、スピン流の発見(というのかどうか?)によってMRAMというイノベーションが起きていますが、絶縁膜が中間膜の場合にも、多層の効果が以前から認められています。ここでは、この効果について、まとめてみます。まずは、基礎的な知識の解説から始めます。
1. 磁壁の構造
軟磁性材料では、反磁界を減らすために図5-1,5-2に示したような磁区構造ができます。特に一軸磁気異方性があるときには、比較的整然とした磁区構造となり、それぞれの磁区の境界には、磁壁ができます。図5-1に示したように、磁壁の中では、磁気モーメントが急激な回転をして、隣り合う磁区の境界になっています。図5-1の場合には、隣り合う磁区は磁化の方向は反平行になっているので、磁壁の中では、磁気モーメントが180°まで回転しています。これを180°磁壁と呼んでいます。磁壁には180°磁壁のほかに、90°磁壁などがありますが(参考文献9a—1)、ここでは省略します。図9-(a)は、180°磁壁内部の構造です。この急激な回転には、二つの磁気エネルギー(自由エネルギー)が関与しています。一つは、交換結合エネルギーで、隣り合う磁気モーメントは平行であれば、このエネルギーは低い、しかし磁壁の中では磁気モーメントは隣の磁気モーメントと平行でなくなるので、交換結合エネルギーが高くなる。自然の法則として、自然エネルギーが低下する配置になります。つまり、なるべく平行になろうとすれば、できるだけ磁壁を厚くして、つまり隣の磁気モーメントとの角度差を小さくしてエネルギー密度を下げればよいのですが、これができないのは、もう一つの磁気エネルギーである磁気異方性エネルギーがあるからです。今は、一軸磁気異方性を考えていますが、磁気モーメントが容易軸から離れて回転しているので、これもエネルギーが高まっています。これを下げるには、容易軸から離れている磁気モーメントの数をできるだけ少なくする、つまり、磁壁をできるだけ薄くしたい、となります。つまり、磁壁の厚さは、この二つの磁気エネルギーの和が最小になる厚みが自然にできます。
では、この話を数式で扱って、磁壁の厚みを出したいと思います(詳細は(参考文献9a—1)にあります)。
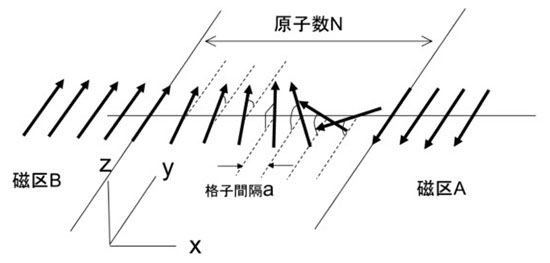
図9a-1
図9a-1は、一軸磁気異方性を持つ材料の中の磁区Aと磁区Bの間の磁壁の内部です。格子間隔 a の原子面(y - z の面)が N 枚並んでいて、その面内の磁気モーメントは、A から B に向かって少しづつ回転します。その隣り合う面の磁気モーメントの回転の角度差はいつも同じと仮定して α とします。厳密には、α は x の位置によって変化しているのですが、計算では一定とします。磁壁内の原子面の数をNとすると、α=π/Nで、Nは非常に大きい値(数10~数100)なので、α は小さい値になります。
ここで前置きです。第9章で説明したように、強磁性金属の中では、磁気モーメントはほとんど電子のスピン S から来たものなので、磁気モーメントは m = -γS(γ:ジャイロ磁気係数、第2章)の関係になります。また、交換結合エネルギーは、磁気モーメントでなく一個の原子が持っているスピン(角運動量)の合計で表し、交換結合エネルギーは、以下のようになります。
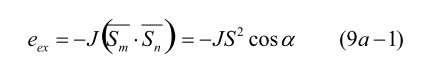
J は、交換結合エネルギー定数、Sm、Sn は隣り合うスピンの大きさと方向です。α は、このスピンの間にある角度差です。第2項の括弧内はスカラー積ですから、平行の時が一番大きく、マイナスの符号が付いているので、平行の時が一番エネルギーが低くて安定、すなわち強磁性、ということですが、今は磁壁の中ですから、平行ではなく α だけ角度差があり、第3項のように cos α が付いてきます。α は小さいので、
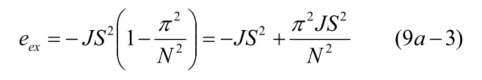
この式の第1項はスピンが平行の時、第2項は α だけ角度がある時のエネルギー増加分を表しているので、第2項が磁壁があるために生じる磁気エネルギーになります。そこで第1項は無視します。磁壁の単位面積にある原子の数は、x - y 面では( 1/a )2、厚み方向がNなので、N/a2 となり、単位面積あたりの交換結合エネルギーは、
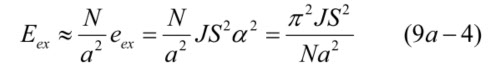
次は、磁気異方性エネルギーです。第4章の(4-1)では、一軸磁気異方性エネルギーは、
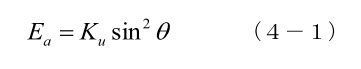
これは、磁気モーメントが容易軸から角度 θ だけ傾いた時のエネルギー増加分を表しているので、各原子面での増加分を全部足し算すればいいのですが、ここでは面倒くさいので、平均すればそれぞれ Ku/2 位だろうということにします。すると磁壁の単位面積では、厚みは Na なので、

Eex + Ea が最低となるような厚み Na は、
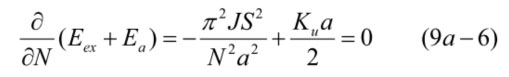
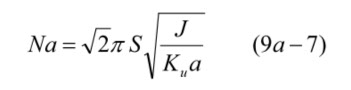
Naは、磁壁の厚みですから、実際にどれくらいになるか、試算します。
第9章で見たように、Fe の磁気モーメントの大きさは、2.2μB なので、スピン S = 1とします。
Jは、磁気モーメント間の結合の強さで、キュリー温度(結合が熱振動エネルギーに負ける温度)から推定できます。これが J ~ 0.02 eV とします。Feの結晶磁気異方性は立方対称なのですが、一軸磁気異方性と同じ異方性定数とすると、Ku = 4x104J/m3 になります。さらに格子面間隔を a = 1.5Å とすると、結果は Na~150Å になります。磁壁の厚みは、これくらいですから、材料内の欠陥や空隙がこれより大きいものが分布していると、磁壁がこれを乗り越えるのが難しくなり、ピン止め、と呼ばれます。これに構わず外部磁界を増やすと、ピン止めが外れて、磁壁はジャンプして動きます。容易軸方向のB-Hループを注意深く見ると、この不連続な動きがループの線に見えます。これをバルクハウゼン効果と呼び、磁性材料が発生する雑音として有名です。ピン止めは、軟磁性材料では特に役に立つ現象ではありませんが、永久磁石材料では重要です。磁気異方性が非常に強いので、(9a-7)からもわかるように、磁壁が非常に薄く、またエネルギー密度が高いので、強力なピン止めが起こり、磁壁が動きません。「ピン止め効果による永久磁石」というのがこれです。
以上のように、磁壁の厚さは、J の大きさ(キュリー温度の高さ)と磁気異方性の強さが釣り合って決まります。軟磁性材料は磁気異方性が弱いので比較的厚く、逆に永久磁石材料は薄くなります。
しかし薄膜では、もう一つの要因(反磁界エネルギー)が入ります。図9a-2は、薄膜の磁壁の断面の図です。(a)は、上で取り扱った構造と同じですが、磁壁内の磁気モーメントが上を向いているので、膜面に垂直方向に磁束の漏れがあり、反磁界が出てきます。(b)は、薄膜の厚みが薄くなった場合で、(a)の構造では反磁界が強くなりすぎるので、磁気モーメントが薄膜の面内で回転するようになります。
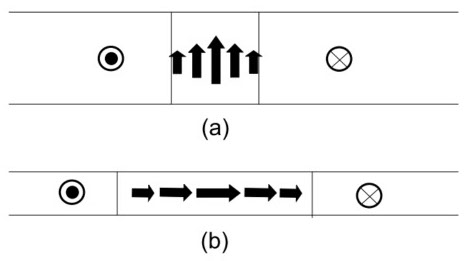
図9a-2
(a)をBloch(ブロッホ)磁壁、(b)をNeel(ネール)磁壁と呼びます。この二つの磁壁と厚みの関係は、上記の計算に、さらに反磁界エネルギーの項を加えます。反磁界係数は、磁壁の厚みと薄膜の厚みから、その矩形の断面を楕円に近似して、(参考文献3—3)から算出します。その計算例(Ni82Fe18 の薄膜)が図9a-3です。
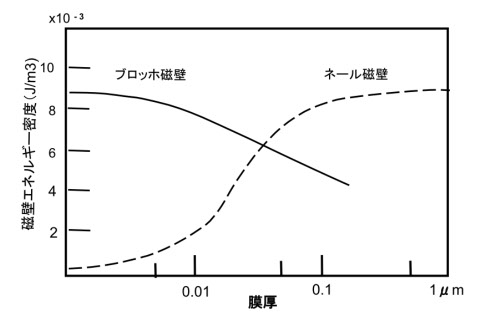
図9a-3
縦軸は単位面積あたりの Bloch と Neel の磁壁エネルギー、横軸は膜厚です。約400Åを境にして、厚い方ではBloch,薄い方では Neel になりますが、その境界付近では、両方が入り混じった Cross Tie(クロスタイ)構造ができます(参考文献9a-2)。
以上が、磁壁構造の基本です。次は、中間に絶縁層を挟んだ軟磁性膜の磁壁について説明します。
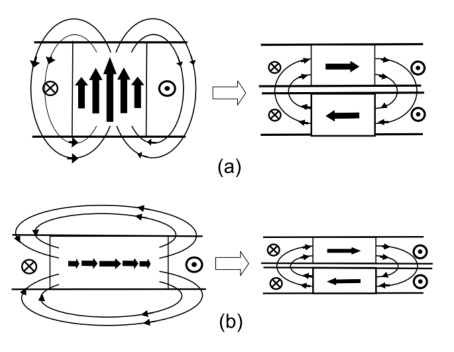
図9a-4
9a-4は、同じ厚さで中間膜が入ったときの、ブロッホ磁壁とネール磁壁の構造の変化です。
1(a)のブロッホ磁壁では、中間膜が入ると、磁束の漏れが少ないネール磁壁の対になります。また、もともとのネール磁壁(b)も、同じ理由でネール磁壁対になります。このネール磁壁対になるかどうかは、中間膜の薄さによるので、中間膜が厚くなると、ネール磁壁対はできなくなります。図9a-5は、ネール磁壁対のできる条件を表しています。
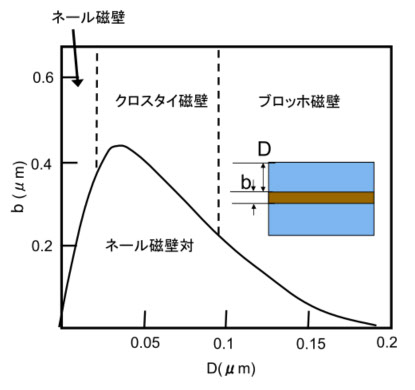
図9a-5
図では、中間膜bが薄くなると、ネール磁壁対ができやすくなり、ブロッホ磁壁とネール磁壁の中間になるクロスタイ磁壁もネール磁壁対になります。磁性膜一層の厚み D が厚くなると、b が薄くてもネール磁壁対ができにくくなります。これは、D が厚くなると、漏れ磁束の量がネール磁壁対でも多くなり、ブロッホ磁壁と変わらなくなるからです。では、ネール磁壁対になると何かいいことがあるか、というと、ネール磁壁では、外部磁界による磁壁の移動が容易になります。その理由は、磁壁の幅が大きくなり、欠陥があっても、磁壁全体が引っかかる確率が下がること、また上下の磁性層が欠陥による磁束の漏れの増加を補いあう機構もあるようです。しかし、正確なモデルはできていません。その結果、容易軸方向の磁化曲線(図5-5参照)の Hc が低下します。
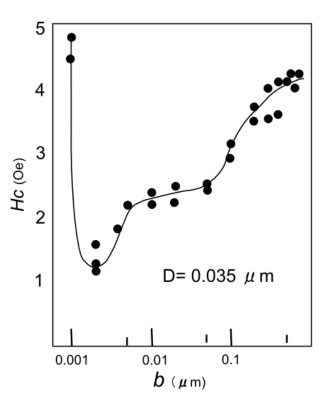
図9a-6
図9a-6は、磁性膜(Co-Zr-Nb)一層の厚み D を 0.035μm に一定として、中間膜 bを変えた時の容易軸方向のHcの変化を測定した結果です。b が約0.002μm(20Å)位までは薄くなると Hc が低下します。20Å以下では、中間層が膜になっておらず、上下の磁性膜がくっついてしまうので、Hc は上昇し、2D の厚みの磁性膜の Hc になります。
第6章では、薄膜はもっぱら困難軸方向で使うと言いましたが、ネール磁壁対も困難軸で使うと、いいことがあります。
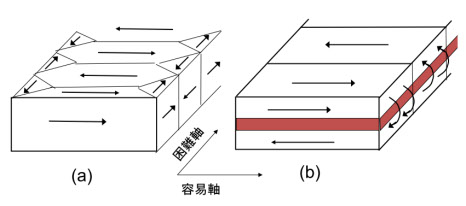
図9a-7
図9a-7は、数10~数μm幅のマイクロ素子の軟磁性単層膜 (a) と二重膜 (b) の磁区構造です。第3章では薄膜の面内方向では反磁界は非常に小さいと書きましたが、それは厚みに対して薄膜の面積が非常に大きい場合で、図9a-7のように厚みに対して面積が小さくなると反磁界が効いてきて、薄膜の端部では磁化が端部と平行になるような磁区構造になります。薄膜を困難軸方向に使うという原則からは、この平行部分は死んでいます。薄膜が小さくなればなるほど、この部分は大きくなるので、高透磁率膜は、マイクロ素子には使えないことになりますが、(b)のような構造では、外部に漏れる磁束量が少ないので、磁区構造が改善されて困難軸方向で使える面積が広がり、薄膜を小型化しても高透磁率が保持できるようになります。
もう一つの利点として、渦電流損失の低下があります。多層膜を構成する磁性層の厚みを、第6章で説明した表皮厚みよりも薄くすると、渦電流損失が大幅に低下します。これについては、別の機会に詳述したいと思います。
以上が多層膜の利点ですが、この原理が実際にたくさん使われているかと言うと、磁気センサーなどには時々応用されていますが、残念ながらあまり多くありません。軟磁性薄膜素子の小サイズ化で最も関心の高いのは超小型インダクタですが、これが意外にうまく行っていない。
しかし最近になって、実用できる薄膜インダクタを作った、と主張している一連の発表があり、それには多層膜が使われています。「補足Ⅱ 薄膜インダクタ」にその概要があります。本当に実用に近いかどうか、考えながら読んでください。
▲ページ上部へ