株式会社東栄 磁気応用部
サイトはこちら
磁気の話のはじめに
1.電荷と磁荷
2.磁気モーメントと磁性材料
3.反磁界と磁化特性
4.強磁性体
5.軟磁性材料
6.磁性材料と高周波
7.微粒子材料
8.磁気の計測
9.スピントロニクスについて
補足Ⅰ 多層膜の軟磁性
補足Ⅱ 薄膜インダクタ
補足Ⅲ 微粒子の透磁率
補足Ⅳ も一度反磁界
参考文献
磁性材料・磁気工学入門
© 2019 Yutaka Shimada

2-1. 磁気モーメントと角運動量
ループ電流にせよ、スピン運動にせよ、質量のある電子の回転運動から生じているわけですから、磁気モーメントは、この力学的角運動量が原因であることになります。そこで、この力学的角運動量とその結果である磁気モーメントを関係式で結んでしまうと、なかなか便利なことになります。たとえば、ある原子のある電子軌道の角運動量がわかれば、その磁気モーメントがわかる、原子の周りの電子軌道はエネルギーの低い順からデジタル的に埋まって行きますから、電子軌道の角運動量もデジタル的に確定できます。すると、軌道磁気モーメントの方向と強さ(ベクトル量)も角運動量から予測できる、となります。スピン磁気モーメントも同様ですが、その詳細は少し後で触れます。
磁気モーメントと角運動量の関係を理解するために、(1-10)式に角運動量を導入します。
円軌道上にある電子が作る角運動量 L は、
ここで、f = ω/2π
(1-10)、(2-1)から
この式では、磁気モーメント m と角運動量 L が結びついています。その比例定数 γ = ( μ0e/2me ) を、磁気回転比(ジャイロ磁気係数)と呼びます。
さらに、μs = γh ( h:プランクの常数) とすると、μs は磁気モーメントの次元となるので、磁気モーメントの基本単位(μB:Bohrmagneton)を、これで定義します。

μB を使うと、軌道運動による磁気モーメント morb は、

電子の軌道は量子化されているので、L もとびとびの値になり、対応する morb も μB を基本量にしてとびとびの値になります。
話を戻しますが、軌道角運動量L に加えて、スピン角運動量を考えなければなりません。その総和は、複数の電子軌道のそれぞれに係る角運動量とスピン角運動量の総ベクトル和になります。スピンについては、「パウリの排他律」が、「各軌道に割り当てられる電子は二個で、お互いに逆向きのスピンを持つ」、と決めているので、ベクトル和、といっても、それぞれの軌道上でキャンセルされます。図1-4に、その様子を描いてあります。しかし、磁性体は、一個だけの電子が孤立している複数の軌道を持っています。Fe、Co、Ni では 3d 軌道群、レアアースでは 4f 軌道群です。外部から見えるスピン磁気モーメントは、これらの不対電子スピンのベクトル和です。
ちょっと頭越しですが、軌道角運動量Lによる磁気モーメント morb が(2-4)であるのに対し、スピン角運動量による磁気モーメント ms は

となります。これは、スピンの自転による角運動量S(スピン量子数)が、(±1/2)の値しか取れず、一方、それに対応するスピン磁気モーメント ms の基本単位は、±μB以下でないので, 2倍することになります。で、スピンの量子数が s =(±1/2)となる理由ですが、量子力学によると、量子数と状態の数 N の関係は常に、
であるので、スピン角運動量では N = 2(各軌道でプラス、マイナスの二つの状態しかない)となると、s =(±1/2)になってしまうのだそうです(参考文献2-1)。これ以上は、著者の知識から離れてしまって生半可な解説になってしまうので、このままにします。興味ある方は(参考文献2-2)をあたってください。
(2-4)と(2—5)が違っているために、角運動量の総量( L とS のベクトル和)と磁気モーメントの総量( morb とms のベクトル和)との関係は、ちょっと複雑になります。
角運動量の総和を J 、磁気モーメントの総和を M とすると、
J = L + S (2-7)
M = morb + ms = -μB ( L + 2S )/h (2-8)
そこで、M とJ の関係を一つの式で表すために、(2-8)を
M = -gμBJ /h (2-9)
g = (3/2) + { S ( S+1 ) - L ( L+1 ) }/{ 2J ( J+ ) }
としてまとめてしまいます。g は、J と M の比になっていて、ランデの g 因子といいます。g は、L と S のベクトル和を計算することによって、L と S の関数として表現できます(参考文献2-3)。
しかし実際の材料では、L と S の大きさを明確に予測し、分離するにはかなり高度な実験と理論が必要です。特に、この話の主な対象となる材料(Fe,Co,Niなどの遷移金属強磁性体)では, 前にも触れたように結晶格子からの電場によって、L ≈ 0 となっているため、(2-9)は(2-5)に近づき、g は、大体 2 に近くなっています。つまり、遷移金属磁性材料の磁気機能性を担う主役は、電子のスピンになります。
ずいぶん長々と磁気モーメントの話をしましたが、このような基礎的知識は、もっと現場に近い分野、例えば、磁性デバイス開発研究などで常に必要か、といえば、必ずしもそうでもなく、忘れていても当面は何とかなる現場も多い。例えば、トランスの鉄心に使う電磁鋼板の磁気損失や、低周波のインダクタ、磁気シールド材など、技術磁化とも呼ばれる分野では、いちいち磁気モーメントのミクロな振る舞いまで気にする必要はありません。
しかし、絶対に理解しておきたいことは、
①単磁極は存在せず、円電流(+電子スピン)を磁気モーメントとして扱う。
②磁気モーメントの根源は力学的角運動量(電子の円運動とスピン運動)から
来るものである。
なぜにこれを強調するか、といえば、①は、磁性材料特有の「反磁界」の理解に繋がり、②は、磁気モーメントの時間的変化(動的変化)、つまり、磁気モーメントの動的振る舞いは、力学的角運動量の動的振る舞い(コマの運動)であり、高周波磁気工学(というものがあるとして)では、この角運動量の動特性が支配的要因になっているからで、技術磁化の分野でも、「磁化の角運動量的な振る舞い」が突然目の前に立ちはだかる時に備えて、十分に理解して置く必要があります。
①については、第3章「反磁界と磁化特性」と「補足Ⅳ も一度反磁界」で詳述します。また②については、以下にその磁気モーメントの力学的角運動量(コマ運動)が剥き出しになっている典型例を説明します。
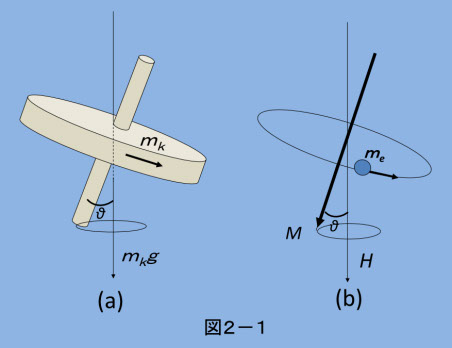
2-2. 磁気モーメントの磁界中での運動
まずは、コマ(コマ回しのコマです)の自転による角運動量がある時に、その重力場中の運動を見て、磁気モーメントの磁界への応答を理解したいと思います。 図2-1(a)は、コマの運動を表しています。図ではコマには重力によって下向きの力が加わり、コマには自転による角運動量があるので、歳差運動(すりこぎ運動、precession)をしています。図2-1(b)は、磁気モーメントが静的な磁界中にある場合を示しています。磁気モーメントも、その根源は電子の軌道円運動とスピンの回転運動、つまり角運動量ですから、磁界によって下向きの力を受けると、磁界中で(a)と同様な歳差運動(すりこぎ運動)をします。磁気モーメントの方向が下向きになっているのは、(2-8)でマイナスがついているからです。
さて、(b)の歳差運動の角速度 ωL と磁界 H の関係は、以下のようになります。これは、(a)のコマの歳差運動周波数と同様の方法で導かれます。詳細は、(参考文献2-4)をあたってください。

磁気モーメントと角運動量の関係をつなぐ量( M/L ) は、(2-2)の磁気回転比 γ になります。
従って、
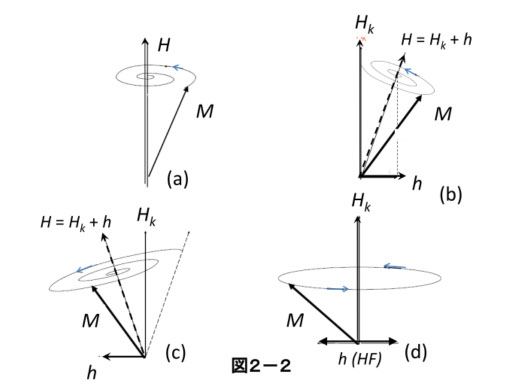
図2—1(b)では、磁気モーメント M は、磁界 H の中で歳差運動を続けて、M と H は角度 θ を保っています。しかし、実際の磁性材料の中では、 θ は時間経過とともに小さくなり、最後は M//H 、つまり磁界の方向を向くことになります。これは、磁性材料中の歳差運動にはエネルギー損失があるからです。一般には磁化は磁界の方向を向く、と言われますが、瞬時に方向を変えるわけではなく、歳差運動が減衰して H 方向に落ち着くまでの時間経過があるわけです。図2-2の(a)に、 M//H になる様子を模式的に示しています。
次は、磁界も時間変化している、すなわち交流磁界、さらに高周波磁界になったら磁気モーメントはどうするか、を説明します。まず前提ですが、磁界の周波数が上がると、磁界の振幅は小さくなります。その理由は、交流磁界は周波数が高くなると(およそ数KHz以上)、大振幅にするのが工学的に難しく、利用価値が低下する。さらに高周波領域数(およそ10MHz以上、10GHzくらいまで)になると非常に弱くなり、通信工学の領域になる、つまり電波として利用されるからです。非常に大雑把ですが、最大で数 10 A/m 程度、通信工学ではもっともっと微弱磁界(電波)の話になります(地磁気は、約 50 A/m です)。
ちょっと驚きですが、通常の強磁性材料の磁気モーメントは、このような微弱磁界にも敏感に反応します。図2-2(b)、(c)、(d) は、磁気モーメントの歳差運動と交流磁界の関係を表しています。
(b)は、(a)で M//H になった後、微弱な交流磁界h が直角方向にある瞬間を表しています。この時、磁界 H は、Hk に変えてあります。理由は、この運動は磁性材料の中の磁気モーメントを想定しているからで、材料中では、外部からの磁界に加えて、材料特有の磁気的性質(磁気異方性)による有効磁界(異方性磁界)Hk があるからです。磁気異方性にもいくつかの種類があり、その実効的な強さを Hk に換算して考える必要がありますが、その詳しい説明は第4章にゆずります。特に軟磁性材料(高透磁率材料)では、高周波磁界中で Hk が大活躍をするので、早めではありますが、Hk を有効磁界の代表にしておきます。
(b)では、交流磁界 h の変化が磁気モーメント M の運動に比べてゆっくりであるとすると、M は歳差運動をしながらHk とh のベクトル和の方向( Hk + h )に落ち着こうとします。次に(c)のように h が変化して反対方向になると、また歳差運動をしながら新しい( Hk + h )の方向に向かいます。さらにhの変化が早くなって(高周波化して)、歳差運動の角速度ωと同じになった場合は、(d)のように、h が駆動源になった歳差運動になり、その振幅が大きくなります。つまり、(2-11)の歳差運動の角速度ωL と h の角速度が一致したときに、磁気共鳴が起こります。磁気共鳴は、磁気モーメントの根源が角運動量であり、その運動の基本は歳差運動であることから起こる現象です。磁性材料が共鳴を起こす周波数領域では、透磁率に大きな変化が起こり、磁気共鳴周波数が、磁性材料の周波数限界になる、という見方もあります。しかし、最近ではこの透磁率の劇的な変化を工学的に利用する研究も進んでいます。なお、この透磁率の動特性については、「第6章 薄膜の透磁率」で詳しく出てくる筈です。
このように磁気モーメントが角運動量であることから来る現象は、磁気工学のうちの高周波磁気工学ともいうべき分野の基礎になるものであり、また最近目覚ましい進歩が始まったスピントロニクスの基礎でもあります。この原稿の最終ゴールは、このあたりになりそうなのですが、そこに到達するには、いろいろ道筋をたどらねばなりません。以下は、その道筋の第一歩です。
2-3. 帯磁率、透磁率
実際の物質中の磁気モーメントは、磁界に反応して、多かれ少なかれ磁界の方向に向きを変えようとします。これは、たとえば「 Fe が磁界中で磁化する」、は、磁気モーメントが磁界の方向に揃う、ということです。もう一度繰り返しますが、図2-1で説明した磁気モーメントの歳差運動は、このままでは永久に磁界の方向に揃わないことになりますが、現実には、この歳差運動にはエネルギー損失があって、図2-2(a)のように一定の時間後には磁界の方向を向きます。この損失は、磁気モーメントが方向を変えると、結晶格子がわずかに伸びたり縮んだりする効果(磁気弾性効果)や、格子欠陥や不純物の存在によって、不規則な歳差運動になる効果、などによって、歳差運動が損失を伴うために起こります。そうして、図2-2で見たように、一定の時間後に磁気モーメントが磁界に平行に揃うことになりますが、現実の材料では磁気モーメントが磁界と完全に平行になる例は少なくて、たいていは、多くの磁気モーメントが磁界の強度に応じて、適当な方向に向きを変えるだけです。それには様々な理由があって,例えば、図2-2(b)では、外部磁界 h に対して、物質の実効磁界 Hk が邪魔をしています。詳細については、ここではとても説明する余裕がないので、今後、機会あるたびに説明をします(第4章、第5章)。そこで、磁気モーメントがどの程度磁界の方向に向くか、が物質の帯磁率 χm になり、いろいろ有限の値を持っています。
真空だけの場合は、磁気モーメントはないので帯磁率は χ0、そこに磁気モーメントを持つ材料の帯磁率を χm として、
透磁率は、
真空の透磁率を μ0 ( = χ0 ) として、比透磁率 μr = μ ⁄ μ0 、比帯磁率 χr = χm ⁄ χ0 を考えると、
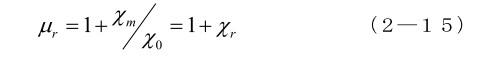
となります。比透磁率は、真空の透磁率との比なので、使う単位系に関係なく同じ値になり、現場の議論には便利です。また、(2—15)でわかるように、比透磁率と比帯磁率の差は 1 であり、材料の比透磁率が数10以上になる場合には、工学分野では比透磁率だけで話をしてもかまいませんが、(2-15)の関係は記憶して置く必要があります。例えば、非常に体積の小さい試料(例えば薄膜)の比透磁率の計測実験などで、空間の比帯磁率(=1)を忘れて思わぬ誤差に繋がったりします。また、周波数が上がって数 GHz ~マイクロ波帯になると、透磁率が小さくても重要な材料になるので、その時は、真空の(実際は空気中の)透磁率を加味した議論になります。たとえば、高透磁率磁心に巻いたコイルのインダクタンスL は、単純なモデルではコイルの巻数 N、断面積 S、透磁率に比例し、そのインピーダンス ZL は、
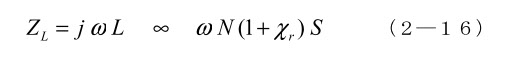
ここで、f = 2πω が非常に大きいと、真空の帯磁率が重要になり、χr がなくても大きなインピーダンスになります。 さらに、χr は小さくてもインピーダンスには結構一人前に効くことになります。低周波では比帯磁率が 0.5 ではまともな磁心材料になりませんが、GHz 以上になると興味深い研究対象になります。実際、マイクロ波帯でそこそこの透磁率を持つ材料は限られていて、新たに見つかれば貴重品(あるいは珍品)扱いになります。
2-4. 磁気モーメントの集合体(すなわち磁性材料)
今までの話は、単一の磁気モーメントについてでした。この節では、磁性材料の中ではどうなっているのか、について説明を始めます。
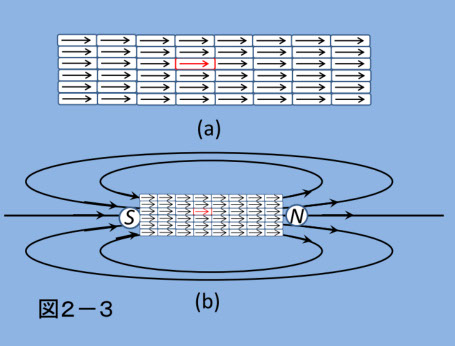
磁性材料中では、1-5で触れたような不対電子軌道(電子が2個乗っていない軌道)を持つ原子(磁性原子)は、ある大きさの磁気モーメント M があり、単位体積(現在は m3 )中の磁気モーメントの集合から出てくる磁束の総量が、その材料の I(磁化の強さ)になります。磁気モーメントの集合体を単純な絵にすると、図2-3(a) のようになります。図では、全ての磁気モーメントがある方向に平行に揃っていて、実際にはあり得ない状態ですが、説明のためにこのように仮定します。これに近い状態が実現できるのは、1-3で触れたレアアース磁石( Fe-Nd-B など)ですが、完全に平行になるわけではありません。また、本稿の主題である軟磁性材料では、コイルを巻いて直流電流によって外部磁界を作らないと、図のようにはなりませんが、外部磁界があると説明が面倒になるので次章に廻し、ここでは永久磁石的なものを考えます。
図2-3で、集合体の内にある一個を取り出します(図中の赤)。この磁気モーメントからは、図1-2に示したのと同じような磁束が出ています。同じような磁束がそれぞれの磁気モーメントから出ていて、隣近所の磁束の分布を強め合ったり、打ち消し合ったりしていて、結局のところ、外部の磁束分布は、図2-3(b) のように集合体が一つの大きな磁気モーメントになった時の分布と同じになります。
その磁極の密度は、
n: 端部の面に垂直な単位ベクトル
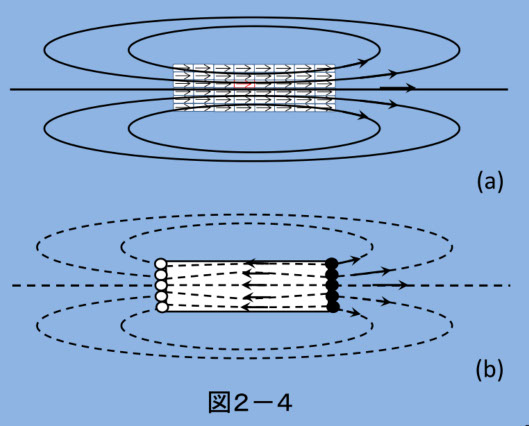
となり、磁極の大きさは端面に垂直な磁束のベクトル成分と同じ値にします。この磁極 σ を使って磁束、磁界の分布を計算した結果は、個々の磁気モーメントが作る磁束、磁界を計算し、全部の磁気モーメントの磁束を合計した結果と同じになります。しかし、これは集合体外部に限っての話で、内部では、現実の磁束の方向は磁気モーメントの向きそのものになるから、磁極を想定した場合の N⇒S の磁束にはなりません。図2-4にその様子が描いてあります。
では、なぜ磁極を想定すると便利か、ということですが、磁極を想定すると、磁界分布が集合体内外ともに計算できるからです。図2-4は、実際に起きている分布を模式的に描いたもので、(a)は磁束分布、(b)は磁界分布で、集合体内部では、磁界の分布は逆方向となります(この逆方向の磁界は、図2-3で個々の磁気モーメントからの磁界を合計しても同じことになります)。さらに、(2-17)に基づいた磁極を想定すれば、磁極のモデルによって磁界の計算が正確にできます(端部における I の分布を正確に求める必要があります)。
以上から、磁極を想定すれば、磁界分布を正確に求めることが可能です。しかし、磁束は、磁界の作る磁束(真空の磁束)と本来ある磁気モーメントの磁束の和になります。磁束に何が起きているかというと、divB = 0 が成り立つ限り、磁気モーメントが密集して磁束密度の高い磁性体内部と透磁率が μ0 しかない外部の磁束を繋ぐには、内部の磁界 Hi が逆方向になって -μ0Hi の磁束を作って磁束の引き算をして、端部で増減のない( divB = 0 を保つ)連続的な磁束密度を作っている、と言うことです。
繰り返しますが、図2-4では、現実の磁束、磁界の関係を単純化して示しています。(a)の実線は磁束、(b)の点線は、磁界です。磁極(白丸、黒丸)を想定すれば磁界分布が得られます。しかし、厳密には(2-17)による正確な磁極分布の情報が必要です。
で、この内部の磁界ですが、図2-4(b)の磁極は、実際には端部の角の影響もあるので不均一に分布し、正確な理論式を作るのは難しいです。が、端部の真ん中あたりの、角から十分に遠い点では、以下のような見積もりができます。

図2-5の材料内部では、

外部では、

磁界については磁極モデルが有効なので、図2-5では黒丸で磁極を表し、磁界の分布を考えます。磁極で作られる磁界は、端部に近ければ
また、divB = 0 より Bi = Be であるので、

この -Hi が、B の連続性を保つために生じる反対方向の内部磁界(参考文献2-5)、すなわち「反磁界」です。ただし、端部近傍での反磁界の大きさを表したに過ぎません。端部に磁極 N があれば反対側には S があり、各々の分布によって、外部の磁界、内部の反磁界が分布します。磁気工学では、この反磁界が材料の磁化特性を決めるので極めて重要な問題になりますが、この内部反磁界の分布をいちいち計算していては話がすすまないので、ざっくりと定数を使って処理することが多くなります。この反磁界定数の使い方については、第3章で詳しく説明します。
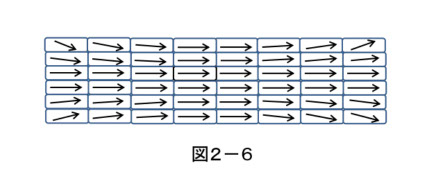
さて、図2-3のモデルは、「磁気モーメントの集合体」としてきましたが、実際の材料でこのような磁気モーメントの配列に近いものは、上でも触れた永久磁石材料( Fe-Nd-B など)です。図2-6は、もっと現実に近い磁気モーメントの分布です。
永久磁石材料は非常に強い「一軸磁気異方性」によって、個々の磁気モーメントが一軸性(ある軸に沿って正負の方向のみがエネルギー的に最低になる)を持っています。この一軸異方性による実効的な磁界(一軸異方性磁界)があるので、磁気モーメントが一度その方向を向くと、放置しても磁気モーメントは動かない、つまり永久磁石になります。この一軸磁気異方性の実効磁界は、単に磁気モーメントの方向をロックしている役割だけなので、(2-18)~(2-21)の議論では出てきません。
永久磁石の磁気モーメントは強い「一軸異方性磁界」の環境下にありますが、図2-6では、この一軸異方性磁界に抵抗して、磁気モーメントの方向がエネルギー最低の方向からずれています。なぜこんな分布になるかというと、外部磁界、外部磁束の空間分布による磁気エネルギーの増加を、磁束のループを最短にすることで最小限にしたいという自然の力が働くからです。外部の磁気エネルギーというのは、
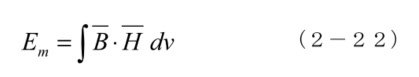
これを全空間に亘って合計したものが、磁束分布の磁気エネルギーですが、これを最小限にするために、集合体の中で磁束が外部のループに繋がるように、磁気モーメントの方向が平行からずれます。
これをもっと数値的に正確に計算するには、(2-22)の空間積分、集合体内での磁気モーメントの方向ずれによって生じる磁気エネルギーの増加、の総和が最低になるように計算します。図2-7はその例で(参考文献2-6から引用)、図2-3のような整然とした磁気モーメントの配列ではなく、端部では図2-6がもっと歪んだ配列になり、磁力線(磁束の方向と密度を表す)も大きく湾曲します。
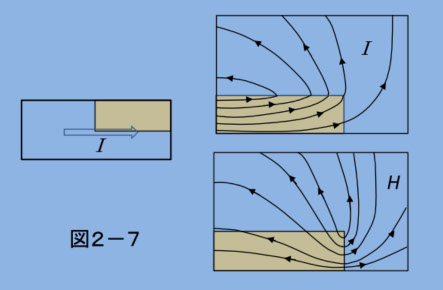
しつこいようですが、磁界の分布は磁性体(集合体)内部では、磁束の方向と大きな違いがあり、端部を境にして磁界の方向が異なります。これは、divB = 0 が成り立つ限り、磁気モーメントによる磁束密度の高い磁性体内部と、磁束密度が μ0He の外部を繋ぐには、磁界が逆方向になって -μ0Hi を作って磁束密度の連続性を維持しているからです。この結果、図2-7でもわかるように、磁性体外部では、B と He の分布は全く同じ( B = μ0He の比例関係)であるのに対し、磁性体内部では全く異なる分布になります。
この磁気モーメントの集合体に対して、集合体内に逆方向に発生する磁界 Hi を「反磁界」と呼び、一般に Hd と表します。また、磁性体に磁界を印加して(磁界の印加、というのは磁気工学ではよく使います)少しずつ強くしていくと、磁気モーメントの磁界方向に向く割合がふえていきます。これは「磁性体が磁化して行く」、と言う表現を使います。この過程では端部の磁極の密度も増えていくので、比例して反磁界も増えます。(2-17)から、端部の磁極の密度は、端部を通る I に比例しますから、
と表して、比例定数の Nd を反磁界係数と呼びます。
今まで説明してきた「反磁界」は、端部のI の分布や、そこからの距離によって異なり、図2-7のように複雑な分布になることも多いのですが、(2-23)はこれを一つの係数にまとめています。随分と乱暴な話ですが、磁気工学では、こうしないと「反磁界」を取り扱いにくいので、止むを得ないやり方、と思ってください。もちろん、必要ならば、図2-7のような数値解析をする手段もあります。
ところで、これまで「磁気モーメントの揃った集合体」を考えてきましたが、実際の材料では、磁性体、特に強磁性材料がそれに相当します。「磁性体」は、非常に曖昧な名称で、磁気モーメントを持っていれば全て磁性体とも言えるので、厳密にはある種の有機物まで入ってしまいますが、ここでの主題は Fe、Ni、Co およびその合金などの強磁性材料なので、磁気モーメントの配列がミクロに見ると隣と平行を保っている、室温以上まで磁気モーメントの配列が崩れない(キュリー温度が室温より十分に高い)、磁気モーメントの密度(磁化の強さ、または飽和磁化)が、応用材料に十分な大きさのものとします。これまでは、「磁性体、磁性材料」をあいまいなままで使ってきましたが、以後、「磁性材料」が出てきたら、そんな定義の材料と受け取ってください。
なお、以上の話は、図2-3、2-4、2-6のような、材料の磁気異方性によって磁気モーメントが自然にある方向に揃っていて、その時に磁束と磁界がどのように分布するかを考えたものです。つまり、これは永久磁石のような材料の場合で、軟磁性材料の場合には外部から磁界を印加して磁気モーメントを揃えることになるので、さらに外部磁界を入れて反磁界を考えます。これを次の章で扱います。
▲ページ上部へ