株式会社東栄科学産業
磁気応用部サイトはこちら
磁気の話のはじめに
1.電荷と磁荷
2.磁気モーメントと磁性材料
3.反磁界と磁化特性
4.強磁性体
5.軟磁性材料
6.磁性材料と高周波
7.微粒子材料
8.磁気の計測
9.スピントロニクスについて
補足Ⅰ 多層膜の軟磁性
補足Ⅱ 薄膜インダクタ
補足Ⅲ 微粒子の透磁率
補足Ⅳ も一度反磁界
参考文献
磁性材料・磁気工学入門
© 2019 Yutaka Shimada

1. スピントロニクスとは
「スピントロニクス(Spintronics)」は、磁性物理とエレクトロ二クスが混在する最新の磁気工学です。このHPの縄張りではないので、専門のHP解説に任せた方がいいように思えますが、軟磁性材料が関与する新分野でもあり、IT分野のハード面で画期的な innovation を起こすかも知れない潜在力を持っいて、全然触れないのもなんとなく納まりが付きにくくなってきました。著者は、学会発表など近々の情報を容易に収集できる立場でもないので、情報が少し古いかもしれませんが、スピントロ二クスの由来が理解できる程度の基礎知識を盛り込んでおきます。
まず、スピントロニクスの発端となった、巨大磁気抵抗効果 GMR(Giant Magneto-resistance)ですが、一口に言えば、ある積層磁性薄膜の磁化の方向によって、電気抵抗が大きく変わる(数10~数100%)効果です。これは、第8章のAMRよりも1~2桁以上大きい効果で、GMR(Giant Magneto-resistance)と呼ばれています。また、TMR(Tunneling Magneto-resistance)は、さらに高い効果とさらなる向上の可能性、また一段の微小化が見込める効果で、これについても紹介し、どのようなインパクトを現在のエレクトロニクスに与えるか、を書こうと思います。
この二つの効果は、Fe、Co、(Ni)、およびその合金の金属強磁性が主役です。説明には、これまで触れていなかった磁気物性的な知識も必要ですので、ちょっと長くなりますが、以下、基礎的な事項を順番に説明していきます。要点だけですので、もっときちんと勉強したいときは、(参考文献9-1)などを見てください。
2. 巨大磁気抵抗効果(GMR)
図9-1は、原子核の周りの電子軌道の配置と名称です。内側から、[1s]、[2s、2p]、[3s、3p、3d]、[4s、4p、4d、4f]、[5s…]と名前が付いていて、各軌道に一対(二個)の電子が入り、そのスピンは互いに反平行になっていて、軌道の数は、sは1本、pは3本、dは5本、なので、入れる電子の数は、sには2個、pには6個、dには10個になります。
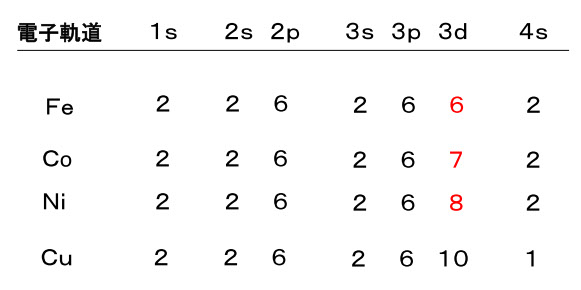
図9-1
図のCuでは、3dまで満杯に入り、4sが一個だけになっています。これに対してFe、Co、Niでは、3dがまだ空いていています。この赤字で示した3d電子の軌道への入り方が特別で、外部から見える磁気モーメントの原因になっています。通常は、各軌道に2個ずつ電子が入り、スピンは反平行なのですが、3dでは図9-2のように、スピンがなるべく平行に並ぶように一個ずつ入り、数が余るとスピンを反平行にして二個の電子が入るようになります。この一個だけでスピンを外部に見せている電子は不対電子と呼ばれ、Fe、Co、Niなどの遷移金属では、外部から観測できる磁気モーメントを、この3dの不対電子のスピンが担っていて、さらに交換結合によって、周囲の原子の不対電子の磁気モーメントと平行になり、さらに、これが室温でも安定……これが強磁性です。
次に、 3d の軌道磁気モーメントについては、Fe、Co、Ni 遷移金属中では普通は無視してしまいます。理由は以下です。
図9-1でわかるように、この 3d 電子群はFe、Co、Ni 遷移金属原子の最外殻付近にあるので、Fe、Co、Ni 遷移金属内では結晶格子からの電場に曝されて、電子の動き(軌道)が格子の対称性に沿った形で拘束されています(軌道の縮退が解ける、といいます)。この時には、3d 電子は第2章で説明したようなループ電流を作る確率が大きく低下し、軌道角運動量はスピン角運動量に比べて非常に小さくなります(参考文献9-2)。ですから、Fe、Co、Ni 遷移金属系では、磁気モーメントの大きさについてはスピン磁気モーメントを数えれば、一応、事足りることになります。(では、第2章の解説は無駄かというと、そうではなく、レアアースでは、最外殻が 6s なので、不対電子がある 4f は、電子軌道群の非常に深いところにあるので、格子電場の影響がなく、ループ電流は拘束されずに生きていて、スピン、軌道の両方の磁気モーメントを数えると、実験事実と非常によく一致します(参考文献9-3)。また、Fe、Co、Ni 遷移金属の軌道磁気モーメントも、非常に小さいですが生き残っていて、結晶の対称性、周期性を持った電場の方向依存性をスピンー軌道のcoupling(スピンー軌道相互作用(参考文献9-3)を通してスピン磁気モーメントに伝達しています。これが、第4章の結晶磁気異方性、および磁歪定数の方向依存性(λ100、λ111など)になって現れているわけです。)
Fe、Co、Ni の 3d 軌道にある電子の数は、それぞれ 6、7、8個です。その外側には 4s 軌道に2個のs 電子があって、電気伝導を担っています。この 3d 電子のスピンの方向については、フントの法則というのがあって、同じ方向のスピンの数を多くするよう配置されるので、その並び方は、図9-2のようになります。
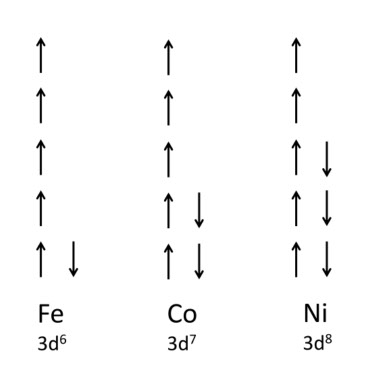
図9-2
図9-2を見ると、Fe の原子あたりの磁気モーメントの大きさは、各原子の 3d 電子の不対スピンの数になります。Fe、Co、Ni は、それぞれ 4、3、2 μB(Bohr Magneton)なります。
これは、フェライトなどでは、そのまま使えます。フェライトでは、Fe は酸素 O-と電荷をやりとりして 4s 電子2個を失って Fe2+、さらに 3d 電子一個も失って Fe3+となっていますが、そのスピンの数と相対的な方向を足し引きすると、Fe2+は 4μB、Fe3+は 5μB となり、Fe2+、Fe3+の格子配置とスピンの方向を考えると、フェライトの飽和磁化(単位体積中のスピン磁気モーメントの総数)が説明できます(参考文献9-4)。このような足し算ができるのは、Fe の 3d 電子軌道が Fe 原子周辺の狭いところに局在し、図9-2のモデルが使えるからです。
しかし、電気伝導性のある遷移金属では、話が全く異なります。もともと 3d 電子は、遷移金属原子の最外殻付近にあり、その外側には4s電子が二個のみです。金属の中では、この4s、3dが電子の海を作っていて、原子はその海の中で格子を組んでいます。これが金属結合であり、その電子の海が電気伝導を担っています。つまり、3d電子は原子の近くに居る確率は高いのですが、同時に格子間をわたり歩いています。これを遍歴電子といいます。こうなると、フェライトなどで役立った純粋な局在電子のモデル、つまり、それぞれの原子の3d軌道のスピンを数える方法は意味がなくなり、電子の海の中のスピンが平均してどっちを向いていて、それが外からどう見えるか、がその金属の磁気モーメントになります。このような金属(Fe、Co、Ni、またその合金)の磁気モーメントの実測値は、原子の電子総数に対する原子一個あたりの磁気モーメント(Slater-Pauling 曲線(参考文献9-5))で整理されています。それによると、Fe、Co、Niは、それぞれ 2.2、1.7、0.6 μB となります。(フェライトと比べると、フェライトの方が磁性が強い(飽和磁化が大きい)ように見えますが、フェライトは、磁性イオンの持つ磁気モーメントが互いに反平行に並んでいて、その差の磁気モーメントが現れるので、また半径の大きい酸素がいっぱいあるので、単位体積あたりの飽和磁化は小さいのです)
この実測結果については、いろいろなモデルで説明が試みられてきました。その内もっとも一般的なのが、以下のバンドモデルです。
孤立した遷移金属の原子では、それぞれの軌道が固定されたエネルギーレベルにありますが、金属結合の中では、3d電子は格子間隔や対称性によって決まる周期的な電場の中で、いろいろなエネルギーレベルを持って動き回っていて、そのエネルギーレベルには大きな分布ができます(参考文献9-5)。図9-3は、孤立原子の固定された電子軌道のエネルギーレベルが、格子の周期性と対称性を持つ電場の中では、遍歴電子が存在し得るエネルギーレベルが多くなり、格子間隔に依存して幅広くなって行く様子を表しています。
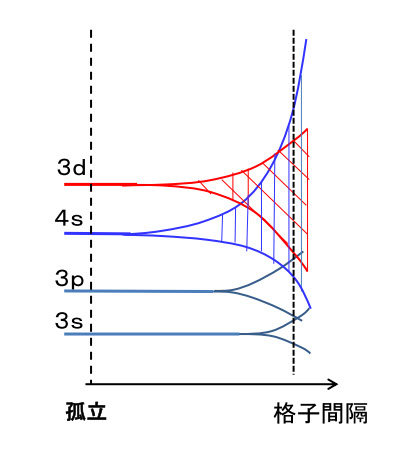
図9-3
図9-3の広がったエネルギー分布の中で、3d電子はどのレベルにどれだけの数が存在し得るか(状態密度といいます)、また、スピンの分布はどうなっているか、については、精密な計算ができます。図9-4(a)は、Feについて計算した3d電子群のバンド構造です。
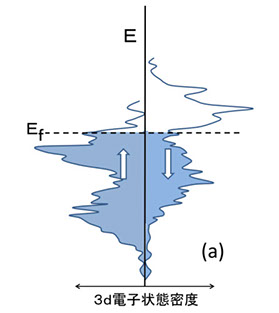
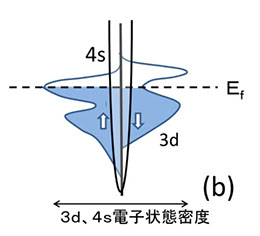
図9-4
縦軸は、各電子のエネルギーレベル、横軸は、そのエネルギーレベルに存在できる電子数の割合(状態密度、Density of States、DOS)です。右側が下向きスピン、左側が上向きスピンをもつ電子の状態密度です。このように状態密度のエネルギー依存性(バンド構造)は、非常に精密に計算できますが、図9-4(b)のように、えいや、と近似しても磁性の定性的な変化は説明できるので、よくやる方法です(Rigid bandmodel)。図9-4(b)の 4s は元々は2個の電子が入っていますが、金属中では Ef(フェルミレベル)直下で自由に動き回り、電気伝導を担っています。また、図9-4の3dバンドは、上向きスピンと下向きスピンが分離していて、しかも縦軸のエネルギー位置がずれています。これは、遍歴電子でも、スピンは交換結合で同方向に並びやすいので、上向き、下向きの二方向のグループに分かれること、また、互いに反対方向のスピンの間では、交換エネルギーが高くなること(第4章)、の二つから、エネルギー位置がずれた2つの集団になります。
図のEf(フェルミレベル)は、遍歴電子群が埋まっている最上部のエネルギー位置を表していて、この付近の電子が電気伝導を担っています。Feの3dは、上向き、下向きのスピンの両方のバンドとも一部がEfの上に出ていて空になっていますが、3d電子にとっては、上向きのバンドの方が居住面積が大きいので、上向きスピンの数が多くなり、その差分が、外から観測できる磁気モーメントになるわけです。これが金属強磁性体の磁気モーメントの根源です。
以上のように、金属強磁性体の飽和磁化(単位体積あたりの磁気モーメント数)は、一個の原子軌道上のスピンを数えるのではなくて、バンド構造によって決まる値になります。
長くなりましたが、まとめると、金属磁性体の3d電子は遍歴電子の性質を強く持ち、バンド構造を持つこと、そのスピン磁気モーメントは、互いに反平行のスピンを持つ二つの電子群のスピン数の差です。 さらに、3d電子は「電気伝導にも参加している」ので、平行、反平行のスピンの数に偏りをもったまま、外部からの電界に応じて動いている、またスピンの偏りを保ったまま外部の金属へも流れ出す、これを利用するのがスピントロ二クスです。
強磁性薄膜2枚を、非磁性薄膜を挟んで積層したときに、強磁性薄膜に何が起きるか、については、古くから研究され、軟磁性薄膜の積層膜では、Hc が低下し、より優れた軟磁性が得られることは、よく知られていました(参考文献9-6)。これは、強磁性薄膜間の静磁的結合によるもので、古典的な効果です。補足Ⅰ 多層膜の軟磁性で詳述します。中間膜が伝導性の場合には、もっと本質的な効果、つまり、上で説明したスピン偏極した遍歴電子が層間を渡り歩いて起こす効果は何かないだろうか、この立場での探索研究がGMRの発見につながり、現在のスピントロニクスの発展の基礎となっています。 ドイツの磁性研究者 P. Grunberg は、この二層膜の層間で遍歴電子が何か起こしていないか、を探す目的で、例えば、Fe/(Cu、Ti、Cr…)/Feのような、遷移金属/金属伝導体/遷移金属の遷移金属二層膜(中間膜を入れると三層膜)を数多く作り、層間の磁気的結合(層間結合)がないかを探索しました。その測定法はBrillowin Scatteringという方法で、磁気モーメントの熱エネルギーによる自然の揺れ(スピン波の素励起)を、光の散乱から測定し磁気モーメントの大きさ、二層膜の磁気的な層間結合の強さなどを算出します。(ちょっと難しいので、手に余ります。これ以上は省略します。) これは、1990年前後の話ですが、当時の薄膜作成法では、数nm程度の薄い中間膜を作るのは、絶縁膜も金属膜も大変に難しく、発表される夥しい数のデータは、サンプルのできの悪さが目立つものが多く、上下の磁性膜が部分的にくっついていたりするために起こる変化がマスクとなり、なかなか出口が見つからない印象でした。筆者のあいまいな記憶ですが、この努力は、10年以上続いています。しかし、粘りに粘っているうちに、他の研究者との共同研究で、Fe/Cr/Feの多層構造に磁界をかけると、電気抵抗が大きく変化すること(巨大磁気抵抗効果)を見つけました。この実験結果は、強磁性体の磁気モーメント(スピン)が伝導電子と絡み合って、何か新現象を起こしている、しかも、工学的にも画期的な機能性が期待できる、ということで世界中の研究者がこの効果を追いかけて、一大ブームとなりました。 この成果によって、P. Grunberg は、2007年のノーベル物理学賞受賞者の一人になりました。
その巨大磁気抵抗効果とは、図9-5のようなものです。
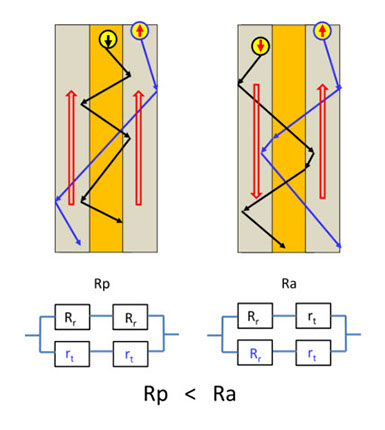
図9-5
二枚の強磁性金属の膜があり、中間には強磁性でない伝導性の中間膜(Cuなど)があるときに、伝導電子が電界によって移動してくると、左の図のように磁化が同じ上向き方向にあると、上向きのスピンを持つ電子は、図9-4の上向きスピンのバンドに入りやすくなります。それは、上向きバンドの方が受け入れ面積(状態密度)が大きいからです。この上向きスピンの電子が感じている電気抵抗を rt とします。一方、下向きスピンを持つ電子は、下向きバンドの状態密度が小さいので、その多くは界面近くで反射して中間膜に戻り、また反射されて……を繰り返します。この時の電気抵抗を Rr として、全抵抗で表すと、図の Rp になります。また、図9-5の右側では、上向き、下向きスピンの電子は両方とも一部反射、一部透過を繰り返すので、等価回路の全抵抗はRaになります。rt は Rr に比べて十分に小さいので、実験では Rp < Ra となり、その差は、10~80%になります。
この抵抗変化の大きさは、第8章で触れたAMRよりもはるかに高く、巨大磁気抵抗効果と呼ばれています。この巨大磁気抵抗効果が起きたということは、強磁性金属の3d電子は、非磁性の導電体中に放出されると、ある距離までスピンの方向性を保持したまま移動できることを表しています。その距離は意外に長く、Cu、Agでは 約100nm以上、Auでは30nm、Pt、Fe 10nm、NiFe 5nm 程度になります。つまり強磁性体/電気伝導体の界面を作り、電流を流すと、強磁性体から伝導体にかなりの距離まで一方向に偏ったスピンを持つ電子群が流れ出す、ということです。これを「スピン偏極電子流」、「スピン流」と呼んでいます。その偏りの度合い(偏極度)は、図9-4の「二つの電子群のスピン数の差」なので、全部の電子が一方向にスピンを揃えているわけではありませんが、最近、偏極度が100%の材料(図9-4で一方のバンドはEfよりも下で満杯、もう一方は Ef よりも上で空っぽ)も見つかって、沢山のグループが研究をすすめています。
これが工学的に意味があるのは、例えば一方の強磁性膜の磁化を固定し(Hcを高くする、固定層)、他の強磁性膜を外部磁界に敏感な軟磁性膜にすると(フリー層)、外部磁界の強弱が,明瞭な電気抵抗の変化に現れることです。図9-6は、その実験例で(参考文献9-7)。
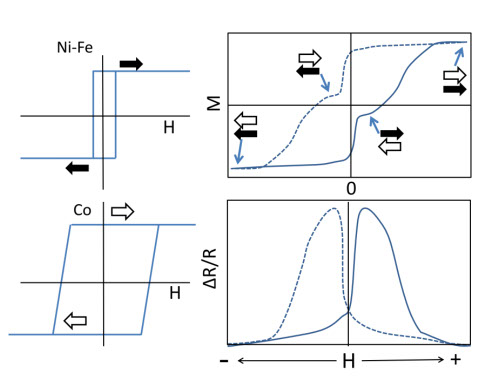
図9-6
CoとNi-Feの間にCuの中間膜がある積層構造で、図のようにCoとNi-FeのHcが大きく異なるので、全体のB-Hループは、段差のある形になります。この段差の肩の部分では、二つの膜の磁化は反平行になり、電気抵抗は図9-7のRa、左右に磁界が強いときは磁化が平行でRpになり、磁界中で抵抗を測ると図9-6のΔR/Rのカーブになります。図9-6の積層構造では、Hcの大きいCoを磁化の固定膜にしていますが、その後は、反強磁性膜を下地にした強磁性膜を固定膜にしています。反強磁性体の役割は、強磁性膜の磁化をある方向に固定するためです。この強磁性体/反強磁性体の界面では強磁性体の磁化がある方向に固定されるという、一見奇妙な効果があり、古くから知られていましたが(参考文献9-8)、磁気異方性の強い反強磁性体で厚い(体積の大きい)下地を作ると、上の強磁性層は、外部磁界がゼロでも一方向に飽和した強固な安定状態になり、強い外部磁界で反転させても、磁界を弱くすると、また元の方向に戻ります。これによって、磁化が一方向に安定した固定膜が作れます(参考文献9-9)。
図9-5では、下から上に向かって(膜面に平行に)電流が流れていますが、これを、膜面に垂直に、つまり図の水平方向に電流を流すと、RpとRaの差は非常に大きくなります(縦方向GMR)。ただし、膜面に縦方向に十分な電流を流すのは大変なので、実験的には薄膜試料を数μm2程度に小さくして電流密度を上げて、電気抵抗変化を検出することになります。実際、縦方向のGMRは、磁気記録での読み出しヘッドに使うために精力的に研究され、ハードディスクの記憶容量は、飛躍的に向上しました。
3. トンネル磁気抵抗効果(TMR)
GMRが発見され、多くの研究者の注目が集まると、さらに、中間膜を絶縁体にした積層膜でトンネル磁気抵抗効果(TMR、TunnelingMagneto-resistance) が発見されました。これは、中間の絶縁膜を十分に薄くして縦方向(膜面垂直方向)に電圧をかけると、3d電子がトンネル効果によって絶縁膜を飛び越えることができて、磁性層間にGMRと同じ効果が起こる、というものです。
このトンネル効果ですが、これは、電子の持つ波動性による純物理現象で、このHPの縄張りをはるかに越えてしまうのですが、行きがかり上、やむなく説明を試みます。
これまで、負の電荷をもつ粒子として電子を見てきましたが、数々の歴史的に有名な実験(Newtonもやってます)によると、電子は波動エネルギーの塊でもあります。図9-7のように、二つの伝導体(青)が非常に狭いギャップ(絶縁層、黄色)を挟んでいる断面を考えます。図は、電子が波動であること示していて、この時、電子の位置はどこなのか、ですが、量子力学では、この波動の形がその存在確率になります。つまり、振幅の中央部は電子がここにいる確率が高く、振幅の小さいところは存在確率が低くなります。ここで大事なことは、存在確率が低くても、辛抱強く何回も測定すると、そこに電子が見つかる場合がある、ということです。図9-7では、二つの場合を描いています。この積層膜には、左方向に電界があって、左側の膜の端部では、夥しい数の電子がギャップにぶつかって反射されています。
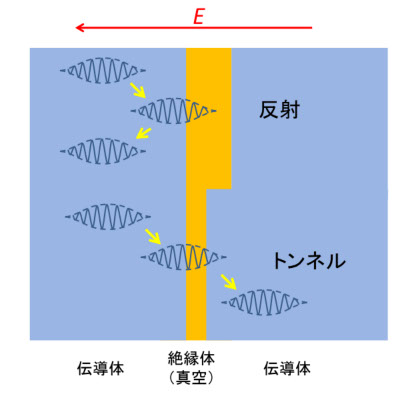
図9-7
この「反射」は、ギャップ内部でも存在確率が見える瞬間がありますが、図の上部のようにギャップが厚いと反射されて戻ります。しかし、下部に示したように、ギャップが薄くなると存在確率が反対側の伝導体にも及ぶようになり、ある回数以上に測定を繰り返すと、反対側の伝導体内に電子が見つかる、ということが起こるのです。このトンネル現象の確率は、もちろん非常に低いですが、夥しい数の電子がこんな状態を繰り返しているわけですから、実験的には、ギャップを通して電流が流れていることが確認できる程度の頻度があり、これがトンネル電流です。ある量子力学の教科書に、「ある厚みの壁に向かってボールをぶつけると跳ね返ってくるが、ある回数以上やるとボールが壁を通り抜けることが一度起こる。その必要回数を計算すると…(忘れましたが、非現実的、途方もない回数)」というのがありました。実際の実験では、中間膜を薄くして電圧をかけると電気伝導が起こり、その電圧ー電流のカーブを見て理論と比較すると、トンネル電流が現実であることがわかります。昔、江崎ダイオードでトンネル効果が発見され、ノーベル賞に輝きましたが、現在のTMRでは、トンネル効果は当たり前のように言われています。これは真空技術、プラズマ工学、薄膜物性計測、材料作成技術の急速な進歩によって、トンネル効果が起こるような精密な積層膜の作成が容易になったためで、総合技術の成果でもあります。
トンネル磁気抵抗効果(TMR)は、縦方向 GMR よりも高い電圧(少ない電流)で抵抗変化が現れるので、応用上有利です。また、電流密度が小さくて済むので、サンプルを極端に小さくする必要もなくなり、応用分野も広がります。さらに最近では、スピン偏極度が100%の材料、またトンネル電子の散乱が少ない(結晶配向性が高い)中間膜などが次々に開発され、抵抗変化率は数100%になっています。
4. GMR,TMRの応用研究
1)磁気センサー
磁気センサーは、パーマロイのAMRで、GPS、エンコーダ、またスマート電力センサーなどの応用がありますが、次には、GMR、TMRに進むのが必然で、すでに実用化の例が出ています(参考文献9-10)。
2)MRAM(Magnetic Random Access Memory)
1960年後半に、軟磁性膜(パーマロイ薄膜)を使って、磁気モーメントの方向を1ビットとして書き込み、読み出すことで、高密度メモリー(任意の場所にアクセスできる Random Access Memory(RAM))ができるというアイディアが提案され、多くの研究者の関心を呼んで、その後10年くらいは一大産業になりそうな勢いで開発研究がすすみましたが、半導体RAMに完敗して消え去ってしまいました。代わりに、磁気テープ(順番にアクセスする Sequential Access Memory(SAM))から始まった磁気記録が飛躍的に拡大して、フロッピー、カセット、VTR,光磁気(ミニディスク)、ハードディスクと入れ代わり立ち代わりに市場に立ち上がり、現在は、ハードディスクが大容量磁気記録技術として定着しています。一方で、半導体フラッシュメモリー(USBメモリー)の発展は今も止まらず、総記憶量100GB以下あたりでは、ハードディスクを追い込みつつあります。 ハードディスクの記録単位(1ビット)は、磁気モーメントの方向(正か負か)で区別し、その体積を小さくすることで記録密度が上げています。しかし、今は1ビットの体積が極限まで小さくなり(約200nm2)、これ以下のサイズでは、熱振動(格子振動その他の熱雑音)に負けて磁気モーメントが不安定になるので(超常磁性といいます)、ここが記憶容量と限界とされています。これを乗り越えるには、1ビットの磁気エネルギーを高める(磁気異方性を強くする、極限の永久磁石材料を使う)しかないのですが、そうすると、外部磁界では磁化反転ができない(磁気ヘッドで書き込めない)問題が出てくる。それでも諦めないで、加熱支援による磁化反転、磁気共鳴支援による磁化反転(下記のスピントルク発信を参照)などが研究され、テラビット/inch2(1012bit/inch2)の世界に挑戦しています。一方、あまり知られていませんが、既に市場から退場したと見られていたVTR的なカセット方式の記録密度が飛躍的に上がっていて、超大容量の磁気記憶方式(一巻で数テラバイト)が開発され、低価格、低消費電力,永続性の特長が生かされて、縁の下の力持ち的に使われています(参考文献9-11)。 その理由は、磁気記録では、磁気モーメントの正負の方向が1ビットなので、他の記憶方式に比べて、不揮発性(記憶保持のための消費電力がゼロ)、および長期間安定保持に優れているので、機械的回転機構が必要なSAMであるにも拘わらず、絶対に消えてはならない超大容量の情報管理、保存などに抜群の信頼を得ているわけです。
この磁気メモリーの恒久的不揮発性と、半導体の高速RAM機能とを併せ持つ磁気RAM(MRAM)の開発が、スピントロニクスの主要な課題になり、1960年代の磁性研究者たちが描いた磁性薄膜RAMの夢が、実現に近づいています。
図9-5で、軟磁性膜の磁化方向を外部から反転させて、その残留磁化方向を1と0のビット情報にすると、そのままMRAMになります。読み出しは、電気抵抗の検出で、また書き込みは外部磁界で可能です。しかし、セルを小さくすること、また書き込み速度を上げることが課題になります。書き込み速度を上げるには、外部磁界の励磁電流を高密度、高速(パルス化)にして、軟磁性膜を高速に磁化反転(ほとんど磁化回転)する必要があります。図9-8は、1ビットのセルのモデル図です。
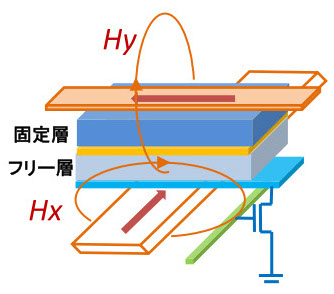
図9-8
書き込みは、直交するHx,Hyのベクトル和でフリー層を磁化反転させて、フリー層/固定層の平行/反平行状態を記憶情報とします。読み出しは、縦方向にセンス電流を流します。しかし、大きな励磁回路、大電流パルスは、小サイズ、小電力の目標に反することになり、MRAM開発は、かつての磁性薄膜RAM、バブル磁区メモリー(参考文献9-12)と同様、頓挫するリスクが見えた時期がありました。
しかし、この難題を解決し、TMRの機能性をさらに拡大させたinnovationが起きました。Spin Transfer Torque(スピン角運動量の転送による磁化反転トルク)とよばれる効果で、先に触れたスピン流を使います。
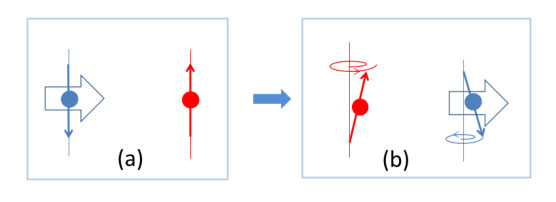
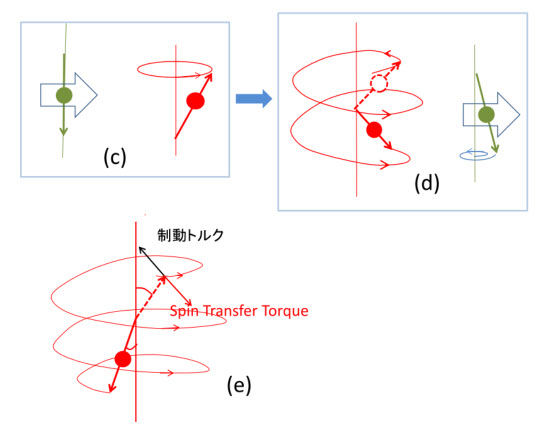
図9-9
スピンとは、もともと電子の角運動量のことで(角運動量と磁気モーメントの関係は第2章)、電子を、自転しているコマとしてイメージするといいかと思います(ただし、第1章で触れましたが、スピン磁気モーメントの大きさは、電子の古典的な自転モデルでは説明できません)。図9-9は、spin transfer torque を定性的に表したもので、著者の不勉強の故に、正確さに不安がありますが、何が起こっているか、は一応表現されていると思います。(a)は、反強磁性下地で磁化を固定した強磁性層のスピン偏極電子を、トンネル層を通ってフリー層へを注入した場合を表しています。赤のスピンはフリー層の磁化方向であり、青のスピンは注入された電子のスピン方向、つまり固定層の磁化方向を表しています。(b)では、注入された電子は、フリー層の電子に近づくと交換結合によって横方向に回転力(トルク)を受けますが、その反作用でフリー層のスピンも横にトルクを受けて、(b)のような歳差運動を始めます。これは、注入電子スピンから角運動量をうけとっている、つまり spintransfer です。さらに、(c)のように、多数の注入電子から角運動量の受け取りを繰り返すと、反対方向(下向き)の安定状態に向かって、スピンが反転します。(e)は、もともとあった制動トルクと、spin transfer torque を表しています。図2-2で説明したように、スピンの歳差運動は、材料のエネルギー損失による制動トルクによって、容易軸(+外部磁界)の方向に落ち着くのですが、図9-11(a)~(d)で表したspintransfer torque は、制動トルクとは逆の方向になり、制動トルクに勝つと、スピンは逆方向の安定軸に向かって反転します。つまり、フリー層から固定層に流した電流(固定層からフリー層に注入された電子群)が十分であれば、フリー層の磁気モーメントは反転して固定層と平行になります。この電流を逆方向に流すと、平行だったフリー層は反転して反平行になります。(この反平行への磁化反転も同じメカニズムですが、ちょっと複雑になります(参考文献9-13))。
単純に考えると、フリー層の電子に、平行でないスピンを持つ電子が近づいた時には、交換結合によってスピン方向が傾くので、複数回繰り返せば反転も起こる、そう考えてはまずいのか、という質問も出そうです。現象的にはそれでいいのですが、スピンは電子コマの運動量、つまり角運動量です。固定層からの偏極スピン電子が近づくと、フリー層の電子コマをむりやり傾かせる力(トルク)が生じます。この時、電子コマは単純に傾くのではなく、元々の方向を軸として歳差運動を始めるだけです。これを繰り返すと歳差運動が激しくなり、ついに反転に至る、ということです。単に磁気モーメントが傾いてひっくり返る、のではありません。
このように、外部磁界の代わりにスピンが偏極した電流を作ると磁化反転を起こせるので、電流駆動のMRAMは実用的には大きなメリットがあります。図9-10は、このスピン注入によるMRAM(Spin RAM)のモデル図です。図9-9と比べると励磁電流の供給線がなくなり、簡単な構造になっていて、励磁による損失や、磁界漏れによる周辺への擾乱もなくなります。
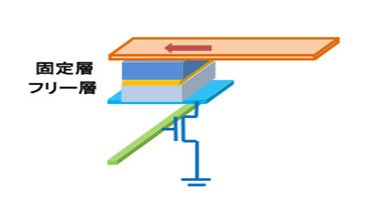
図9-10
図9-9のような、強磁性体から流れ出る電流によって磁化が反転する、というような物理現象が、なぜ最近まで注目されなかったのか、磁性研究の永い歴史から見ると不思議ですが、これには理由があります。
先に説明したように、Fe/Cuの二重層に縦方向(膜面垂直方向)に電流を流すと、FeからCuへ流れ出すスピンの偏極状態はある距離まで続きます。このスピン偏極電子が図9-9の青、緑の電子です。これらの電子のトルク転送で磁化反転を起こせるという原理的なアイディアが、Slonczewskiによって発表され(参考文献9-14)、実証実験も成功しましたが(参考文献9-15)、実は、磁化反転に十分なトルクをフリー層の電子に与えるためには、高密度の偏極電子の注入が必要なのです。その電流密度は約109A/cm2という大きなもので、断面積10μm2の導体では10Aが必要で、実現にはちょっと無理, しかし、100nm2の断面積の導体ならば、1mA位になり、ようやく現実的な値になります。このくらいの微小な素子にならないと、spin transfer torque による磁化反転は起きないので、従来の試料作製技術では到底考えられなかったサイズ領域だったわけです。
この難題を短時間で克服し、実用段階まで持って来てしまった最新の実験技術、理論構築力には、全く驚かされます。最近では、この電流密度を一桁くらい下げた素子も作られています。
従って、Spin RAMは、超高度な薄膜材料・素子作成技術で実現した微小な高機能素子なのです。現在、Spin RAMは、産学共同の多くのプロジェクトで開発がすすめられ、半導体RAMの最大の弱点である「記憶保持動作」が要らない演算素子がどこまで可能か、期待が高まっています。
また、偏極状態が続くスピンの流れ(スピン流)は、偏極という状態を保ったまま、ある距離まで拡散します。この拡散は、電流の分布とは関係なく拡散し、別の強磁性体に達すると、電圧を誘起します。さらに、従来の半導体のキャリアにスピンの情報を入れると、磁性体の記憶機能と半導体の論理演算機能を併せ持つ素子(スピントランジスタ)も可能になります(参考文献9-16)。
3)スピントルク発信(Spin Torque Oscillator, STO)
図9-9の(b)、(c)では、赤のスピンに歳差運動が励起されています。ここでスピン偏極電子の注入量を調節して歳差運動を持続、安定化して、さらに外部磁界によって歳差運動の周波数を変えると、極めて小サイズ、簡単な構造、磁界制御可能な高周波発信素子になります。
図9-11は、その基本構造です。上下間の通電領域(トンネル電流接点)の面積は、直径数10nm程度にして電流密度を上げています(参考文献9-17)。高密度の集積回路にも容易に組み込めることが可能で、カバーする周波数範囲(数10GHz)、サイズの点で、これまでにない発信素子です(参考文献9-18)。
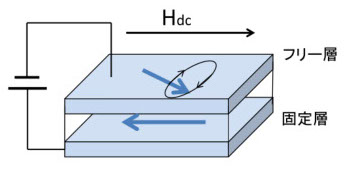
図9-11
このような発信素子の使い道の一つとして、磁気記録(ハードディスク)の更なる記録密度の向上のための書き込み磁気ヘッドへの応用があります。先に説明したように、ハードディスクの1ビットのメモリーの安定化には、磁気異方性の強い記録媒体が必要ですが、そうなると、これまでの磁気ヘッドでは飽和磁化が足りなくてビットが書き込めなくなる、それでも諦めないで、というのは、先に書きましたが、その方法として、磁気ヘッドの先端にSTOを取り付けて、高異方性媒体への書き込みを可能にする方法が研究されています。STOは非常に高い周波数も発信できるので、記録媒体の磁気共鳴周波数に合う周波数を発信すると、磁気ヘッド先端に近づいた媒体が局所的に磁気共鳴を起こし、振幅の大きい歳差運動が始まるので、磁化反転に必要な磁界強度が低下するのです。これが実用化に成功すると、ハードディスクの記憶容量は、現在の1テスラバイト位のものが、10テスラバイト、さらにそれ以上も期待できます。
以上、駆け足でスピントロ二クスを通り抜けました。このHPは、当面、以後の章の企画は無しですが、終わりではなく、読者の皆様のご意見を参考にして、最初から見直しながら内容の充実を図る予定です。よろしく。
▲ページ上部へ