株式会社東栄 磁気応用部
サイトはこちら
磁気の話のはじめに
1.電荷と磁荷
2.磁気モーメントと磁性材料
3.反磁界と磁化特性
4.強磁性体
5.軟磁性材料
6.磁性材料と高周波
7.微粒子材料
8.磁気の計測
9.スピントロニクスについて
補足Ⅰ 多層膜の軟磁性
補足Ⅱ 薄膜インダクタ
補足Ⅲ 微粒子の透磁率
補足Ⅳ も一度反磁界
参考文献
磁性材料・磁気工学入門
© 2019 Yutaka Shimada

5-1. 軟磁性材料の二つの磁化過程
前章で説明したように、軟磁性材料は、結晶磁気異方性や磁気弾性効果が無い,または小さい状態なので、残るのは誘導磁気異方性をどのように使うか、です。誘導磁気異方性は一軸なので、磁化過程としては、容易軸方向と困難軸方向の二つを考えておけば事足ります。
まずは、「磁区」の話です。4-1で説明したように、強磁性体内では、磁気モーメントが交換エネルギーによって強固に結合し、互いに平行な状態になるはずですが、図5-1のように、平行になる領域は「磁区」と呼ばれる限られたサイズになります。隣には別の磁区があり、その境界は、「磁壁」になっています。磁壁の内部では、磁気モーメントが平行でなく、回転しています。4-1で触れた「交換結合エネルギー」+「磁気異方性エネルギー」が最低になる状態(平行状態で容易軸方向)に抗して無理な回転をしているので、非常にエネルギー密度が高くなっていて磁壁エネルギー密度と呼ばれます。磁壁には、Bloch磁壁(180°、90°磁壁)、Neel磁壁など、いろいろありますが(参考文献5-1)、ここでは180°の磁壁を想定します。 どうして磁区ができるのか、ですが、これは反磁界が関わっています。図5-2は、二つの磁化構造の比較です。(a)は、磁性体の磁化が一方向に揃っていて、外部に磁束が広く分布している状態です。(b)は、磁化が交互に反対方向を向いて、外部に漏れる磁束が激減し、反磁界が非常に弱くなります。もし、磁気異方性が弱くて、磁化反転が容易であれば、(b)は自然に出来る構造で、図5-1のような磁区に分かれます。
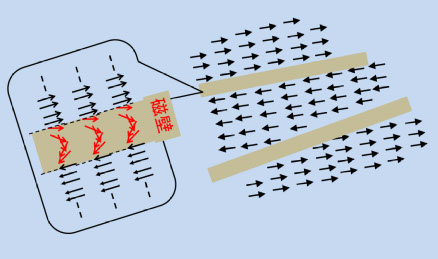
図5-1
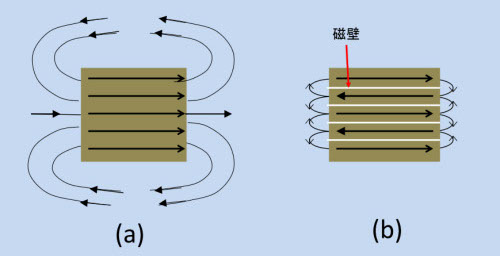
図5-2
図5-3(a)は、Fe-Si(電磁鋼板)の磁区構造で、白の部分の磁化と黒の磁化は反対方向を向いていて、白黒の境目に磁壁が走っています。右半分は、レーザー照射により磁区を細分化して、磁壁の数を増やして動的な損失を低減させています(参考文献5-2)。磁壁と損失については、あとで説明します。図5-3(b)は、80パーマロイ薄膜の磁区観察例ですが、エネルギー密度の高い磁壁は、材料の欠陥や局所的な異方性の乱れがあると、引っかりが生じて動きにくくなる、という厄介な性質があり、特に薄膜では、いろいろな凸凹や構造欠陥、また局所的な歪みなどが多いので、磁壁もあちこちに引っかかり、直線的な磁壁にはなりませんが、基本構造は、図5-2(b)と同じです。
(a)


(b)
図5-3
これに外部磁界を加えると磁化曲線はどうなるか、が次の話です。
図5-4は、軟磁性材料の内部の磁区構造のモデルです。磁化の方向は、ほぼ容易軸方向(図では(a)の外部磁界 He 方向およびその逆方向)を向いています。磁区の境界には磁壁があり、材料に弱い外部磁界が印加されると、外部磁界の方向が磁化の方向に近い場合には、その方向に磁化が向いている磁区の体積を増やすように磁壁が湾曲しますが、これは初磁化過程で、外部磁界が増えると次に磁壁全体が移動を始めます(図5−4(a))。これを磁壁移動による磁化反転といいます。また、磁界の方向が、磁化の方向と大きく異なり、困難軸方向(90°)近くになっていると(図5−4(b))、磁壁は動かず、磁化そのものが磁界の強さに応じて徐々に回転します。これは磁化回転による磁化過程です。
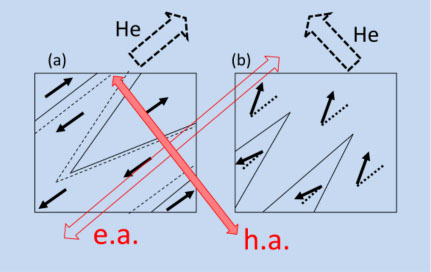
図5-4
材料中には、結晶粒界、格子欠陥、歪、不純物、空隙,材料端部など多種類の磁気的に不均一なサイトが分布していて、磁壁がこれらのサイトを通過しようとすると、磁壁の磁化の分布が乱されてエネルギー極小点に落ち込んでトラップされて、さらに He を増やさないと動き出さない。つまり、磁壁の移動のし易さが、容易軸方向の磁化曲線を決めています。一方、困難軸方向では、磁気異方性磁界に打ち勝って磁化回転を続けるためには、He を増やし続ける必要があります。図5-5は、図5-4の(a)と(b)の方向の磁化曲線のモデルです。
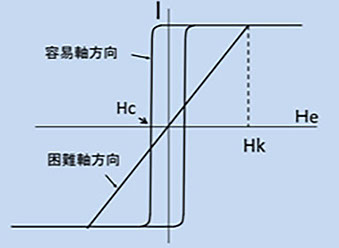
図5-5
図の容易軸( easy axis )方向が磁壁移動による磁化過程で、通常は比較的弱い磁界で磁壁が動きだすので大振幅磁化反転が可能です。しかし、磁壁が動き出すまでにある強さの磁界が必要で、これを磁壁抗磁力( Hw )、また、磁壁が動いて磁化の反転量がちょうど半分になり、外からみると材料の磁化が平均してゼロに見える、つまり消磁状態にあるときの磁界を、抗磁力( Hc )と呼びます。困難軸方向では He の増加に伴って磁化が回転し、飽和(完全に外部磁界方向を向く)に達する時の外部磁界強度が Hk(一軸磁気異方性の実効磁界)と等しくなります。困難軸方向では磁壁移動はないので Hw 、Hc は無い。しかし、困難軸にも Hc が現れる場合があり、容易軸と困難軸が材料内で方向と強さが均一でなく分布がある(異方性分散)と、このようなことが起きます(図4-3は、その例)。一般に異方性の分散は、形状の非対称性や結晶軸の偏り、また歪みの分布(磁気弾性効果)などによって起こります。
磁気工学では、この二つの磁化過程をうまく使い分けます。一般に磁壁移動の磁化過程が使いやすいように見えますが、磁壁移動は移動速度に限度があり、周波数が高くなると動かなくなる。その原因の一つが図5-6です。
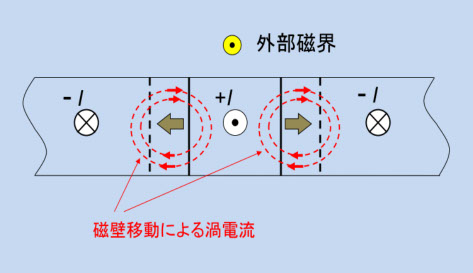
図5-6
容易軸方向で駆動磁界(外部磁界)の周波数を上げると、高速で移動する磁壁を境にして高速の磁化反転が起きて渦電流による熱損失が集中的に起こります。磁壁移動による渦電流損失の計算式と実験(参考文献5-3)によれば、金属磁性材料は厚さ数10ミクロン程度で、磁界 He の周波数が数 KHz 以下であれば、渦電流損失は致命的欠陥にはなりませんが、これ以上の周波数に対応するためには、電気抵抗を上げるか、材料を数ミクロン以下の薄膜にしなければ使えません。さらに薄膜になっても、磁壁の運動自体が慣性と熱損失を伴うので(参考文献5-4)、移動速度には上限があります。磁壁移動による磁化反転の限界は、小振幅の He でも数 MHz あたりになります。
というわけで磁壁移動は高周波には弱いですが、低周波では弱い He で大振幅の磁化反転ができるので、広い用途があります。たとえばFe-Si(電磁鋼板)は、図5-3(a)のような短冊状磁区が並んでいますが、電力変換用変圧器(トランス)の中では、この磁区が交流磁界(50または60Hzの He )に応じて磁壁が大幅に移動して磁化反転が起こっています。この時の磁化反転量は各磁壁が分担するので、磁壁の数を多くすると一個の磁壁が担当する移動距離が小さくなり、その分、移動速度も低速で済むので、図5-6の損失も少なくなります(参考文献5-3)。これが、図5-3(a)の右半分の細かい磁区構造です。電磁鋼板の開発では、この磁区をいかに細かくするか、が重要な研究課題の一つです。
一方、困難軸方向は、図5-5のように磁化曲線が傾くので透磁率が低いですが、磁化回転は第2章で説明した磁気モーメントの歳差運動の結果なので、He の高速変化に対して高速で追随するので、磁気共鳴(数10 MHz ~数 GHz 、Hk によって変わる)が起こるまで透磁率はほぼ一定です。図5-7は、磁壁移動と磁化回転による透磁率の(a)外部磁界依存性と(b)周波数依存性を模式的に描いたものです。透磁率の定義はいろいろありますが、ここでは、微分磁化率( μ = ΔI/ΔH 、磁化曲線各部の傾斜)です。(a)は、外部磁界依存性の容易軸(e.a.磁壁移動)と困難軸(h.a.磁化回転)の違い、(b)はその周波数特性の違いです。なお、h.a.方向でも渦電流損失が無視できない状態、たとえば、薄膜が厚い場合などでは、図5-8のような渦電流が起こるので、周波数が高くなると透磁率が低下します。詳しくは、第6章で説明します。
磁壁移動の透磁率については、いろいろな磁壁移動のモデルが提案されましたが、計算が複雑で標準的な理論はありません。しかし、磁化回転の透磁率は、飽和磁化 Is、異方性磁界 Hk 、電気抵抗、膜厚を考えることによって、渦電流損失、磁気共鳴を含めた理論計算による実験結果の予測、また素子の設計が可能です。理由は、磁壁移動の速度は局所的な構造(欠陥の密度、機械的構造の揺れなど)によって変わるので、計算モデルによって結果が大きく異なるのに対し、磁化回転は材料中に均一に起きるため、図5-8のような渦電流のモデルが現実に近くなるからです。なお、図5-7の μ(h.a.)は、図中の交流磁界(赤矢印)の方向の μ に相当します。数MHz~数GHzで起こるピ-クは、磁気共鳴が起こっていることを示しています。
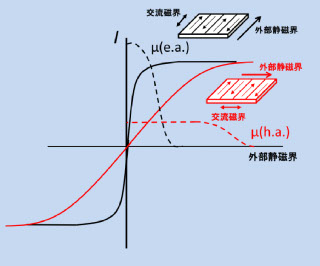
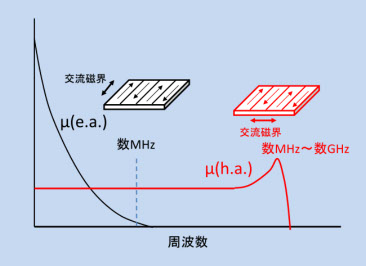
図5-7
(b)
(a)
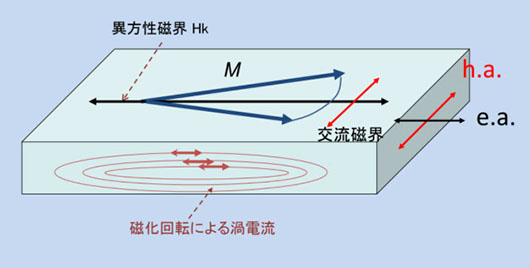
図5-8
なお、薄膜形状であるときは、以下の5-2-1(2)で説明するように、面内の一軸磁気異方性に加えて(3-11)式の形状磁気異方性(垂直方向が困難軸、面内が容易軸)が関与します。このため、μ(h.a.)の磁気共鳴周波数(図5-7(b)赤線)は、バルク材料よりも高くなります。「薄膜の透磁率」については、下の第6章を見てください。
6.磁性材料と高周波
ここで横道ですが、一軸磁気異方性が主役にならない特別な軟磁性材料がありますので、簡単に触れておきます。一つは、センダスト合金で、Fe85Al5.5Si9.5(wt.%)の組成付近で DO3 型という規則型結晶構造になり、結晶磁気異方性、磁歪定数がゼロになり(参考文献5-5)、さらに、誘導磁気異方性もありません。理由は、規則型結晶では原子配置が規則的に固定されているので、Fe原子が格子点を渡り歩く頻度が低く、磁界中熱処理くらいでは磁性原子の再配列が起こらないからです。また、Fe系ナノクリスタル材料(5-2-5)も結晶サイズはナノサイズですが、結晶相であることは同様で、磁界中熱処理で形成される一軸磁気異方性はひじょうに弱く、また分散しています。これらの磁区構造は方向選択性のない複雑なものになり、良い観察例が発表されていません。その結果、等方的に高い透磁率がえられますが、磁壁移動と磁化回転が混在して、周波数上昇に対して単調に低下していく傾向があり(参考文献5-6)、理論的な取扱いは難しくなります。
更に、グラニュラー薄膜で例外的な誘導磁気異方性が見られます。その詳細は下記の5-2-5-bで説明しますが、その一つは Co を含むグラニュラー薄膜(5-2-5に詳述)で、非常に強い Ku (80パーマロイの Hk = 240 A/mに対し 8000~80000 A/m)を示し、詳しいデータが発表されています(参考文献5-7)。二つ目は、Fe系グラニュラー薄膜で、磁界中で薄膜形成すると強い一軸磁気異方性ができます(参考文献5-8)。両方ともに、その原因は完全には解明されていませんが、磁気工学的には、強い一軸磁気異方性によって磁気共鳴周波数がより高くなるので、図5-7(b)の透磁率が一定になる周波数範囲が広くなるので、魅力ある材料になっています。
5-2.軟磁性材料
5-2-1. バルク材料と薄膜材料の相違
これまで、磁化過程などについて、「材料の厚さ」をあいまいにして説明してきましたが、材料の厚さが違うと、磁気的性質(Is、磁歪定数、磁気異方性定数)が同じでも、その軟磁性はバルク材料と薄膜材料では大きな相違があるので、ここで厚さによる違いを整理しておきます。ここでは、材料の厚さ5~10μmを境にして、それ以上をバルク材料、以下を薄膜材料とします。説明の都合上、厚さの影響がより大きい薄膜材料を先にします。
(1)形態の相違
当たり前のことですが、薄膜は基板の上に形成されています。その形成法は、蒸着、スパッター、めっき(化学、電気)が代表的なものです。いずれにしても、磁性素材+添加元素の原子(イオン)が、真空中、放電プラズマ中、反応液中に放出されてのち、基板表面に沈着し固体化する過程になります。この時何がおきるか、を下に列挙します。
基板上で固体化(結晶形成、アモルファス構造形成)する際に、非常に強い応力が発生する。応力発生の原因は主に二つあり、一つは、薄膜材料と基板材料の熱膨張の差、もう一つは、膜表面への原子(イオン)の供給速度に比べて固体化(結晶構造の形成)が非常に遅いので、高密度の欠陥、void が生じ、固体化の進行にともなって構造が歪むことです。固体化を早くするために基板を加熱したりしますが、そんなことではなかなか追いつきません。
しかし、固体化が遅いことを逆手にとって、結晶化をわざと不完全にして軟磁性を実現している薄膜材料が沢山あります。具体例は、パーマロイ薄膜(結晶構造としては、完全な規則相よりも準安定な不規則相であることが軟磁性の必要条件、5-2-3に詳述)、アモルファス合金(結晶構造が存在しないことが軟磁性の条件、5-2-4に詳述)、ナノクリスタル構造(結晶成長をナノサイズに抑える、5-2-5に詳述)など。
要するに、結晶成長が不十分、あるいは皆無であることが軟磁性を良くしているが、基板上に形成されることで、強い応力発生は避けられない、ということになります。
バルク材料では、充分に結晶成長させた軟磁性材料(Fe-Si、Fe-Si-Alなど)と、薄膜と同じく結晶成長を抑えた材料(アモルファ薄帯、ナノクリスタル薄帯)があり、これらは、薄膜のような強い応力の発生もなく、熱処理によって応力除去も容易になります。その結果、Fe-Si、50パーマロイ(Fe50Ni50)などは、軟磁性の条件(Kc=0、λ=0)に完全に合致しなくても軟磁性材料として役立っています。
軟磁性の条件(Kc=0、λ=0)を満足する強磁性合金はたった二つだけで、パーマロイ(Ni80Fe20)とセンダスト(Fe-Si-Al)です。パーマロイは、5-2-3で説明しますが、Ni と Fe の原子が結晶格子点にランダムに配置した無秩序合金相で Kc=0,λ=0 になります。逆に、センダストは規則相(DO3)ができると Kc=0、λ=0 になります。従って、適切な合金相を得るための熱処理条件も大きく異なりますが、ここでは省略します。
(2)反磁界の相違
4-2で説明したように、薄膜は膜面に垂直方向を困難軸とする強い形状磁気異方性(反磁界)、つまり磁気モーメントを薄膜面内に抑え込む異方性があります。また、この稿で扱う薄膜材料のほとんどは、これに加えて、面内に一軸磁気異方性(ほとんどの場合、誘導磁気異方性)があります。(理由は、(1)の準安定軟磁性では、磁界中熱処理によって一軸磁気異方性が作れる、ということです。)その困難軸の磁化過程に関しては5-1に書いた通りですが、この二つの磁気異方性によって薄膜の透磁率、その周波数特性、磁気共鳴周波数などが決まり、また、渦電流などの高周波損失も理論式に組み入れることができるので、理論的な計算も実験値とよく一致し、素子設計に役立ちます。バルク材料は3次元的形状になるので、厚みや形状によって反磁界は複雑になり、詳しく知るには数値計算が必要になります。
(3)損失の相違
軟磁性材料の磁化過程に伴う損失(発熱)の原因は、三つあります。一つは、磁壁移動、磁化回転の際に、欠陥や局所的な応力、また凸凹があると、そこに引っかかってからジャンプして進むので、行きと帰りが不可逆的(違うルートを通る)になり、その分が熱損失になり(参考文献5-9)、ヒステリシス損と呼ばれます。その大きさは、図5-5の容易軸方向磁化曲線の面積に相当します。あとの二つは、図5-6と図5-8の磁壁移動による渦電流と磁化回転による渦電流です。薄膜では、ヒステリシス損は大きくなりますが、殆どの場合、磁化回転を使うので、これは膜厚が薄くなれば、それだけ低下します(第6章に詳述)。これに対してバルク材料では、磁壁移動、もしくは磁化回転も混在するハイブリッド磁化過程になるので、渦電流損失が周波数に対して急激に大きくなります。薄帯形状(厚さ数10μm) のバルク材料の損失については、第6章に以下の記事があります。
バルク軟磁性材料の動的損失
(4)軟磁性の相違
高周波、小振幅(磁化回転)で利用する薄膜は、結晶磁気異方性、磁歪両方ともにほぼゼロであることが必要条件になりますが、バルク材料は、結晶磁気異方性、磁歪が完全にゼロでなくても低周波、大振幅(磁壁移動が主)では使えます。純鉄も電磁駆動制御素子(電磁スイッチなど)の性能向上のために、軟磁性の改善(大結晶粒、低炭素化)がすすんでいます(参考文献5-10)。
5-2-2. Fe-Si
Fe の基本的な磁性は、4-1で説明しましたが、Fe-Si の合金は軟磁性が改善され、電磁鋼板として非常に広い用途を持ちます。Feは、半導体と並んで「産業の米」と言われたくらいの基盤材料ですが、Fe-Si は「コシヒカリ」くらいの位置付けでしょうか。図5-9は、磁歪定数、結晶磁気異方性定数の変化です。図中のλpolyは、Fe-Si の多結晶を想定して、(4-10)を使って計算したものです。Si が約1wt%、6wt%で磁歪定数がゼロ、または非常に小さくなりますが、通常は、高い飽和磁化が優先され、Silwt%以下で使います(従って、磁歪は完全にゼロでないものも使っています)。電磁鋼板の磁化過程は磁壁移動で、Hc は非常に小さく、立ち上がりも急峻で、磁気損失(ヒステリシス損+渦電流損)をできるだけ小さくすることが開発目標になります。電磁鋼板では、特定の結晶軸を長さ方向に成長させたもの(方向性ケイ素鋼板)、結晶軸を均等に分散させたもの(無方向性ケイ素鋼板)があります。Fe-Si の結晶構造は bcc で、磁気異方性も立方晶ですが、図5-3のような美しい磁区構造にするには、結晶軸を揃えて、さらに一軸性の応力を発生させるコーティングにより一軸磁気異方性を作っています。このあたりには膨大なデータが蓄積され、電磁鋼板自体が一つの工学分野と言ってもいいくらいで、方向性の鋼板は磁束の変化が常に一定方向になるトランス、無方向性は磁束の方向が回転するモーターの鉄芯に大量に使われます。図5-9の λpoly は、無方向性ケイ素鋼板に対応します。
ついでながら、最近では、車載モーターの需要が激増し、その小型化(高周波化)が重要な課題となっているので、モーター鉄芯の高周波化(KHz以上)が研究されています。高周波で低損失の高飽和磁化、低損失材料の有力候補は、FeやFe-Siの微粉末です。どうしてそうなるかは、第7章と補足Ⅲを参照してください。
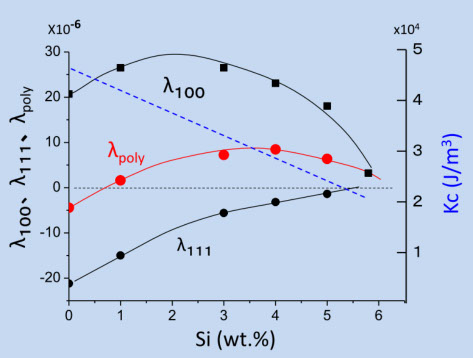
図5-9
5-2-3. Ni-Fe(パーマロイ)
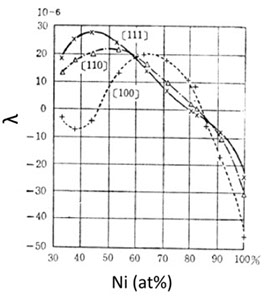
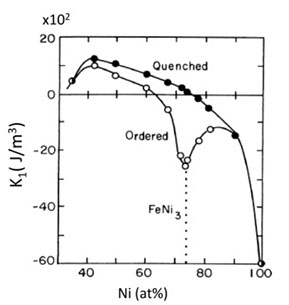
Fe と Ni の合金は、飽和磁化は Fe の半分位に低下しますが、組成によって結晶磁気異方性、磁歪、キュリー温度が大きく変化し、様々な特徴のある合金になります。Fe-Ni(~36at.%)、Fe-Ni(~50at.%)、Fe-Ni(~80at.%)が実用材料です。Fe-Ni(~36at.%)(インバー)は、Tc(キュリー温度)が室温近くに低下している合金で、磁気の消失(磁歪の消失)と熱膨張が相殺して、熱膨張が非常に小さくなる( Fe の10%程度)という特徴があります(参考文献5-11)。Fe-Ni(~50at.%(50パーマロイ)は、結晶磁気異方性定数が 103J/m3 と小さく、飽和磁化の大きい軟磁性材料になりますが、磁歪は大きいので、歪に注意した使い方になります。Fe-Ni(~80at.%)は、結晶磁気異方性、磁歪がともに小さく、最高の軟磁性を持つ材料の一つです。この合金を板状にして巻いたものは、有用な磁気コアですが、機械的衝撃に弱いという弱点があり、現在では機械的強さのあるアモルファス、ナノクリスタル材料が多く使われています。しかし、80パーマロイの軟磁性薄膜は、様々な実用例があり、現在でも工業材料としての位置付けは高いものがあります。Feの室温での結晶構造はbcc、Ni はfccで、bcc-fccの境界は約Ni30at%にあり、これ以上のNi濃度を持つ合金は不規則相(fccの格子点におけるNi、Fe原子の配置がランダム)です。図5-10(a)、(b)は、この不規則相(Quenched)の結晶磁気異方性K1、磁歪定数です(参考文献5-12)。
(b)
(a)
図5-10
これらの定数は、両方ともNiの増加に伴って、Ni80Fe20付近で正から負へと変わり、ゼロを通過します。注意すべき点は、K1とλがゼロを通過する組成が少しずれていることです。薄膜では、Ni82Fe18くらい(λをゼロに近づけた組成)にすることが多いようです。
少しばかり注意すべきことは、この組成領域では 500℃ 付近に不規則 → FeNi3 規則相の変態点があり、非常にゆっくり冷却すると、図5-1(a)の「Ordered」 で示したような FeNi3 規則相が混じることがあります。図のように、この規則相の結晶磁気異方性 K1 は負の値を持ち、軟磁性にはなりません。しかしパーマロイ薄膜の多くは、蒸着法、スパッター法、めっき法で作られるので、膜形成時の実効的冷却速度は非常に早く、規則相混入の心配はまずない。念のため、Moを5%程度加えると、Ni、Fe原子の規則配列を抑える働きがあるので、不規則度が増すので、さらに安心です。
ちょっと横道ですが、知っておくべき事として、80パーマロイ合金の機能性の一つに、伝導電子のスピンー軌道相互作用に起因する異方的磁気抵抗効果(AMR、Anomalous Magnetoresistance)があります。これは磁化の方向によって電気抵抗が変化する効果で、Ni80at%付近では約3%です。このAMR薄膜は、地磁気センサーとしてGPSに組み合わせてスマートフォンなどに利用されています。現在、磁気工学の花形であるGMR(巨大磁気抵抗効果)、TMR(トンネル磁気抵抗効果)薄膜に比べると抵抗変化は遥かに低く、学問的には古典的現象ですが、GMR、TMRが複雑な積層構造の薄膜であるのに対し、パーマロイ薄膜の単層で磁気センサーの機能を発揮する利点があり、今も広く実用されています。この特徴は他の材料には無いので、パーマロイ薄膜が第一線から消えない理由です。
80パーマロイも、図5-3のような、互いに反平行の磁化を持つ磁区が並んでいます。つまり、80パーマロイにも一軸磁気異方性があるということですが、結晶磁気異方性、磁気弾性効果は非常に小さいので、この一軸磁気異方性は、形状磁気異方性を除くと、誘導磁気異方性が原因です。誘導磁気異方性は、軟磁性材料、薄膜の透磁率、磁気共鳴周波数を決める要因になるので、ぜひ覚えていてください。80パーマロイの誘導磁気異方性の大きさは、Hk にして約240A/m(=3Oe)、飽和磁化は1Teslaなので、(4-6)から困難軸方向の比透磁率 μr は3300, 磁気共鳴周波数は約500MHzになります。
繰り返しになりますが、薄膜の形状磁気異方性は、図4-4右図のように、面に垂直方向が困難軸、面内が容易面であり、その容易面内に、さらに一軸の誘導磁気異方性がある、と言うことを覚えておいてください。第6章で、また出てきます。
なお、Fe-Ni薄膜については、以下に詳しい解説があります。
島田:連載講座 軟磁性材料 薄膜Ⅳ「Fe-Ni系軟磁性薄膜」 日本磁気学会
「 まぐね」 (Magnetics Japan)4(5), 246-252, 2009
5-2-4. アモルファス軟磁性材料
これまでの議論でおわかりのように、軟磁性材料の理想的な条件は、結晶磁気異方性、と磁歪定数がゼロであること、また、誘導磁気異方性をうまく制御できること、です。その点で、上記のパーマロイは、まことにうまくできている材料です。結晶材料としては、これ以外には、センダスト(Fe-Si-Al)しかありません。
アモルファス合金は、強磁性遷移金属(Fe、Co、Ni)にガラス化元素(Si、B、P…)を~20at%以上加えた溶融合金を、高速回転するローラー表面に吹き付けることで急冷すると(液相急冷法)、結晶構造のないアモルファス強磁性合金ができます(参考文献5-13)。また、(Fe、Co、Ni)に(Ta、Zr、Nb…)を~10at%以上加えた合金を薄膜プロセス(スパッター法など) で作ると、アモルファス薄膜となります。この合金は、結晶構造がない、つまり原子が方向性や対称性なしにランダムに分布した、いわゆるガラス構造になっています。原子間の結合軸の方向がバラバラなので、というより、結晶軸がないので、結晶磁気異方性はなくなります。図5-11は、その製品の例です(参考文献5-14)。厚さは数10ミクロンのシート状になり、アモルファス薄帯と呼ばれています。
で作ると、アモルファス薄膜となります。この合金は、結晶構造がない、つまり原子が方向性や対称性なしにランダムに分布した、いわゆるガラス構造になっています。原子間の結合軸の方向がバラバラなので、というより、結晶軸がないので、結晶磁気異方性はなくなります。図5-11は、その製品の例です(参考文献5-14)。厚さは数10ミクロンのシート状になり、アモルファス薄帯と呼ばれています。
アモルファス材料では、原子配置(原子間距離も方向も)がバラバラなので、結晶磁気異方性ゼロに加えて磁気弾性効果もゼロ、となればいいのですが、そうはなりません。磁歪はばっちり現れます。「何故でしょうか?」という質問も受けるので、詳しく説明します。
図5-11 日立金属 Materials Magiより
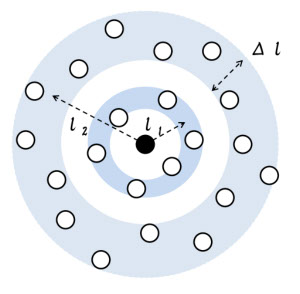
図5-12
図5-12は、アモルファス相の原子構造の模式図です。ある原子(黒丸)に注目すると、その周囲には、同じ磁性原子が無秩序に分布しています(ガラス化元素は描いていません)。しかし、原子間の距離に関しては完全に無秩序ではなくて、ある範囲内に保たれています。図では、最隣接原子の平均距離を l1 、第2隣接原子の平均距離を l2 としていますが、それぞれ l1 +Δl1 、l2 +Δl2 のバラつきで原子が分布しています。ここで重要なことは、Δl1 、Δl2 は意外に小さい値であるということです(図では Δl を誇張してあります)。これは、物質を構成する原子の原子間距離は、「双極子相互作用の引力+電子軌道の反発力」によるポテンシャルエネルギーが最低になるところにあり、その最低値は距離に非常に敏感なので、原子間距離が大きくバラつくことはないからです(参考文献5-15)。となると、アモルファスの磁歪を考えるには、図4-9の磁歪の機構の説明図を少し修正し、原子間相互の方向は完全にばらばらにする一方、原子間距離は Δl の範囲内でバラつかせることになります。これを図4-9に対応して描けば、図5-13になります。図では、消磁状態の磁区構造を描くことは難しかったので、あるものとして想像してください。
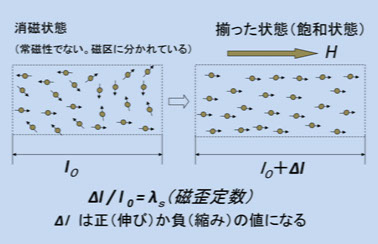
図5-13
図5-13では、図4-9の格子構造の面影を残しているように見えます。それは、原子間距離があまり変わらないからです。実際、アモルファス金属の原子配置は、面心立方対称(fcc)の配置をぼやかしたような構造であることがわかっています。これは、たとえば沢山のビー玉を箱に入れてガラガラと振ると、自然に出来る細密構造は、fcc(立方晶晶)とhcp(六方晶)の混在した配置に近いものになり、ビー玉の相互の距離はある範囲内に保たれることからもわかることです。
もし、原子配置の方向に加えて、原子間距離も広範囲にバラバラであれば、磁歪は正負に分布し、大きさもバラバラで平均はゼロ、となるでしょうが、原子間距離は十分にばらばらでないのです。図5-13を見ると、それが直観的にわかると思います。これが、アモルファス相は結晶磁気異方性が平均化されて無くなっても磁歪の平均値はゼロからずれて残る、しかも、fcc構造の磁歪を反映している理由です。
ちなみに、Feの結晶構造はbcc(体心立方)で、磁歪定数は、図5-9のSiゼロ%の値ですが、アモルファス構造は、fcc的になるので、アモルファスFe-Si-Bなどの磁歪定数は結構大きく、+30~40x10-6(30~40ppm)になります。
そういうわけで、アモルファス構造と言えども、磁気弾性効果から逃げられないのですが、アモルファス材料の軟磁性は、磁歪と奇妙な関係にあります。
まず、アモルファス材料の内、磁歪定数がゼロになる組成((Co95Fe5)80-(Si,B)20,Co86Zr6Nb8)は、もともと結晶磁気異方性が無いので、磁歪もゼロであれば非常に優れた軟磁性となり、厚さ数10μmの薄帯のHcは数A/mのものがあります。地磁気は約40A/mですから、その凄さがわかると思います。では、上に書いた Fe 系アモルファス薄帯(Fe-Si-Bなど)は、磁歪が大きいのでダメ、となりそうですが、実は、結構な常識はずれの軟磁性を持ちます。その理由は、アモルファス合金の機械的性質の均一性にあります。アモルファス相は、結晶粒界、格子欠陥は無し、ミクロな空隙や凸凹も無いので、応力がかかっても歪は広範囲に均一に分布します。それで、磁気弾性効果による磁気異方性も均一になり、局所的欠陥に敏感な磁壁も動きやすくなり、磁化回転も均一に、となります。つまり、応力の方向と均一性に注意し、さらに熱処理で歪を取り除けば、優れた軟磁性材料になります。実際、電力用の変圧器には実用されていて、その変換効率(熱損失の少なさ)では電磁鋼板(Fe-Si)変圧器をはるかに越えています。アモルファス薄帯が世に出た1970年代前半には、その10年後には世の中の変圧器全てが、アモルファス変圧器に置き替わるだろう、と言う夢が語られたほどに凄い材料なのです。現実は、今でもほとんどが電磁鋼板の変圧器で、産業の基盤に根を張った既存技術の寸刻みの進展の凄さを象徴していますが、アモルファス変圧器も数10年の頑張りによって、じわじわと普及がすすんでいるようです(参考文献5-16)。
なお、Fe系アモルファス合金は、歪の均一性によって軟磁性を保持していますが、磁歪定数は大きいので、突発的な機械歪に弱いのはそのままです。お忘れなく。
アモルファス合金には、大別して、液相急冷法による強磁性遷移金属( Fe、Co、Ni )+ガラス化元素(Si、B、P……) および、薄膜プロセス(スパッター法など)による強磁性遷移金属( Fe、Co、Ni ) + Light Metal(Ta、Zr、Nb……)の二つのグループがあります。薄膜材料には、特別な場合(積極的に磁気弾性効果を使うなど)を除いては、磁歪定数がゼロになる組成を使います。理由はすでに5-2-1で書いた通りです。
アモルファス合金の飽和磁化、磁歪の組成依存性のデータは、(参考文献5-17)にありますが、具体的な感触を得るために、図5-14、5-15に概要を紹介しておきます。
(a)
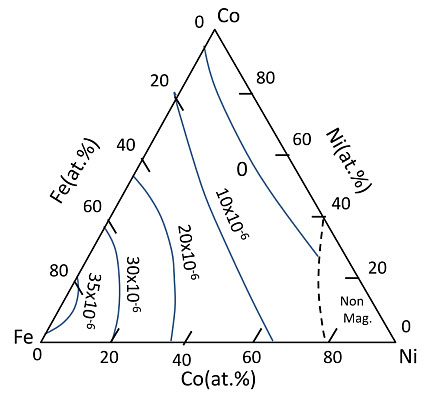
(b)
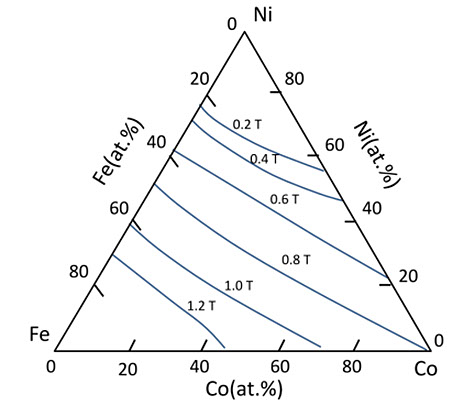
図5-14
図5-14(a)は、(FeCoNi)78Si8B14の薄帯のIs, (b)は、λs です。λs がゼロになる組成は、(Fe5Co95)SiB付近にあり、Is は 1.0 Tesla 位で、80パーマロイと同じくらいですが、結晶粒界も欠陥もないので、軟磁性という点では他を圧倒しています。また、上に触れたように、Fe サイドでは λs が大きいですが、軟磁性材料としては飽和磁化が大きく、Fe-Siに代わる超低損失トランス磁心材料として実用化がすすんでいます。
(a)
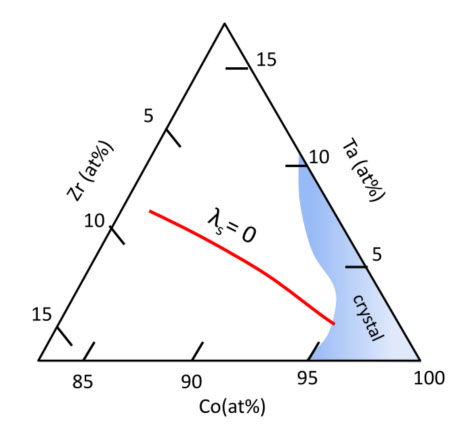
(b)
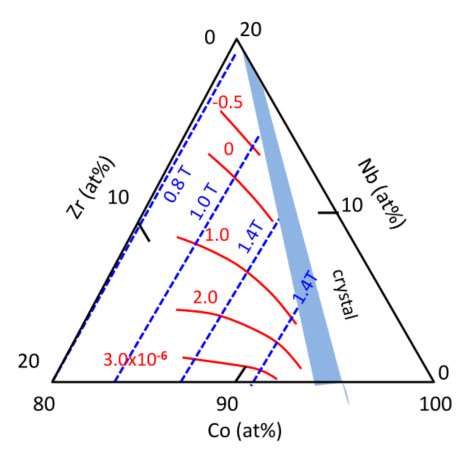
図5-15
図5-15(a)は、Co-Zr-Nb薄膜の Is とλs, (b)は、Co-Zr-Ta薄膜の Is と λs で図5-14の薄帯と比べると、λs の変化が小さいのが特徴で、磁歪の小さい組成範囲が広くとれます。Co-Zr-Taは、アモルファスになる組成範囲が少しばかり広くなります。
このCo系は、液相急冷法で薄帯を作ると、Co-Zr(10at%)付近以外にはアモルファスになりません。スパッター法などの薄膜プロセスのみでアモルファスになる理由は、液相急冷よりも、急冷速度が高いからと考えられています。
現在、薄膜の軟磁性材料として実用されているアモルファス合金の代表組成は、
- (CoxFe1-x)y-(Si-B)1-y
- Co-(Ta,Zr,Nb)
1.は、x=0.95、y=0.8 あたりでゼロ磁歪、2.は、(Ta,Zr,Nb)の比を調整するとゼロ磁歪になります。代表的なものは、Co86Zr6Nb8で、Is = 1Tesla、結晶化温度=約450℃、誘導磁気異方性は Hk =1200 A/m(=15 Oe)、磁気共鳴周波数は約1GHz です。
ここまで書くと、アモルファス材料は軟磁性材料としては敵なし、に見えますが、一つだけ泣き所があります。アモルファス相は、準安定状態のガラス構造なので、ある温度以上では、安定な結晶相に向かって相分解が起こり、軟磁性も機械的強度も失います。その温度(結晶化温度)は、実用材料では400~600℃で、室温では十分に安定です。しかし、飽和磁化を増すために、ガラス化元素を減らす必要がありますが、結晶化温度が低下します。図5-16は、Co系アモルファス合金について、結晶化温度(Tx)と飽和磁化をいろいろな組成についてプロットしたものです(参考文献5-18)。実用性を上げるために飽和磁化を上げると、Tx が低下して不安定になり、組成を動かすだけでは限界があることがわかります。
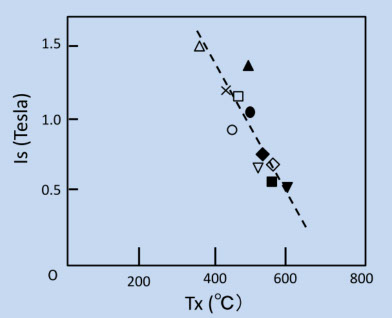
図5-16
結晶化温度が充分高くて、実用に耐えるものとしては、
Fe系でIs=1.5Tesla, Co系で1.1Tesla 位が限界になります。
また、アモルファス合金は、磁性材料としては極めて優れもので機械的強度もあるのですが、構造材としてはあまり用途が広がっていないようです。急冷の方法として水中に吹き出すことで、アモルファス金属繊維も作れます(参考文献5-19)。他の繊維と違って伸び縮みがない。釣りの道糸に最適で、アユの友釣りテストでは、すばらしい感触だったそうです。軽くて強いので飛行機の構造材に使ったら?…という話もあったそうですが、これはちょっとアブなくて乗れない。何かのはずみで結晶化が始まったら一巻の終わりです。
なお、アモルファス軟磁性材料については、以下に詳しい解説があります。
島田:連載講座 軟磁性材料 ナノ構造材料Ⅰ「アモルファス材料・ナノクリスタル材料」
日本磁気学会 「まぐね」 (Magnetics Japan) 4(8), 402-408, 2009
5-2-5. 微結晶材料
5-2-5-a. ナノクリスタル材料
実は、かなり以前から、そのヒントになる話が、いくつか学会で発表されておりました。今から振り返れば、そうだったか…ということで、当時は注意を引かなかった話です。その一つは、「Fe-Siを多層構造にすると Hc が低くなる(参考文献5-20)」というもので、いくつかの発表に共通するのは、材料の結晶サイズが非常に小さくなっている、ということでした。Fe-Si多層膜では、Fe-Siが基板上で結晶成長する厚みになる前に、異物の層(SiO2、Coなど)を挟むことで、Fe-Siの微結晶構造ができる、というやり方でしたが、当時は、結晶サイズとHcの関係が発表データからは明確でなく、何だかわからない……で終わりでした。
微結晶と軟磁性の物理が明らかになったのは、ナノクリスタル薄帯が発表され(参考文献5-21)、その軟磁性と結晶サイズの関係が解明された時です(参考文献5-22)。 図5-17は、ある強さの結晶磁気異方性(この図では一軸)をもつ結晶の集合体(多結晶体)の模式図です(参考文献5-23)。隣り合う結晶の粒界では、隣り合う磁気モーメントの間には非常に強い交換結合(5-1節)があって、磁気モーメントは互いに平行になります。しかし、a)の結晶内部では磁気異方性(点線矢印)が強いので、磁気モーメントはそれに支配されています。それに対してb)では、結晶粒界が沢山あるので、交換結合が支配的になり、結晶内部でも平行にする力が働きます。つまり、結晶磁気異方性は、交換結合に負けてしまって、無いも同然、となるのです。
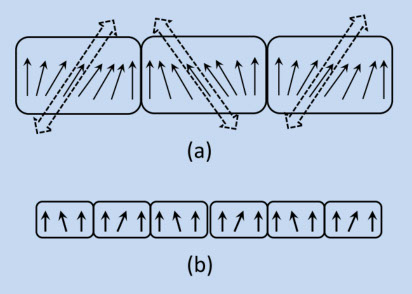
図5-17
この微粒子モデルを使って、粒子サイズとHcの関係を理論的に求めたものが、Herzer のモデルとして知られています(参考文献5-22)。図5-18は、材料の結晶粒子サイズのみに注目して、Hc の変化を見たものです(参考文献5-22)。サイズが0.1μm以下になると、Hcが急激に低下するのがわかります。その低下の傾斜は、D6に比例し、これは Herzer のモデルからも得られる関係で、図5-17の(b)のような状態は、このサイズ以下で起こることがわかります。1μm 以上では 1/D で低下し、結晶粒界の磁壁ピン止めの頻度が減り、磁壁が動きやすくなると説明されていますが、ここでは、あまり関係のないことです。
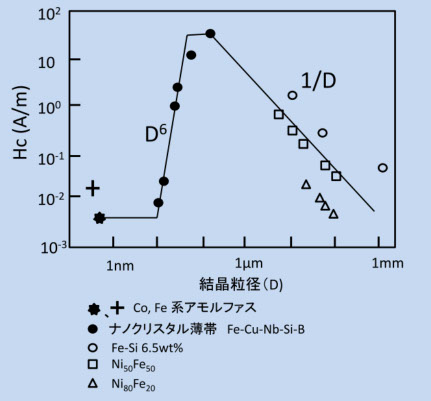
図5-18
図5-18の D6 のラインに乗っているナノクリスタル薄帯(●)は、図5-19のような構造になっていて、図5-17のメカニズムが実現されています。図5-19は、急冷ロール法によるアモルファス薄帯(FeCuNbSi)を熱処理で結晶化、相分離させて作ったナノクリスタル構造の模式図です(参考文献5-24から引用)。
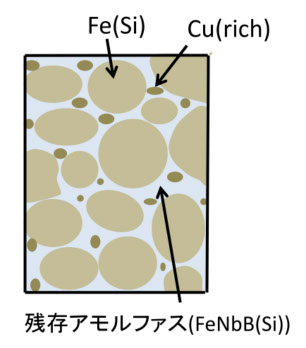
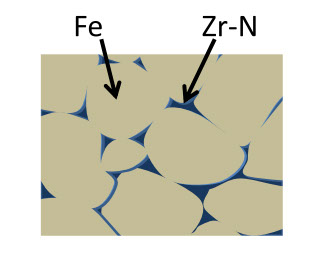
図5-19
図5-20
Fe-Siのナノ結晶がCuの結晶微粒子とアモルファス相によって成長を抑えられ、さらにアモルファス相に残存する強磁性によって、Fe-Si微粒子間に磁気的結合((交換結合)があるので、結晶磁気異方性が見えなくなっている、という軟磁性材料です。スパッター薄膜では、もっと簡単な構造で同じ効果が得られます。例えば、Fe-Zrの薄膜を、Ar+N2の混合ガス中でスパッター法で作り熱処理すると、ZrとNの化合物が先にできて、Feの成長を抑えてナノクリスタル構造が出来上がります(参考文献5-25)。図5-20は、その模式図で、Feの微粒子が互いに接触し、交換結合が強いので結晶磁気異方性は無し、になっています。図5-21は、この時の飽和磁歪定数の熱処理による変化で、Fe 多結晶の平均磁歪が出ていて、適当な熱処理(400℃位)によって、ゼロに近づけることができます。 ただし、微結晶の結晶軸の方向が、平均してどうなっているか、はわからない状態です。
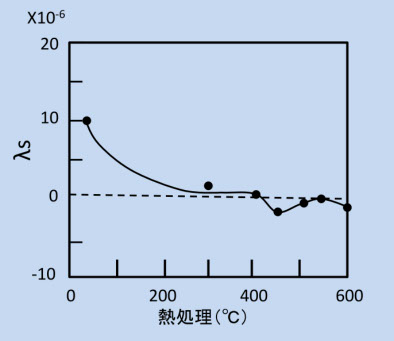
図5-21
以上のように、Fe系アモルファス材料の高い飽和磁化を保ちながら、結晶磁気異方性、磁歪を低下させ、さらに温度に強いナノクリスタル構造ができます。この材料は、アモルファス材料の弱点である温度不安定性を無しにしているので、実用範囲がさらに拡大しています。この薄帯の詳細は、日立金属(株)のweb site (ファインメット)を見てください。
5-2-5-b. グラニュラー薄膜
ナノクリスタル構造では、結晶磁気異方性がゼロ、磁歪が小さい、を実現できることがわかりましたが、慾を出してもう一つの課題、すなわち電気的絶縁性はどうだろうか、に関心が向かいます。
図5-6や図5-8でわかるように、渦電流が泣き所の最たるものです。この HP では触れていませんが、軟磁性フェライトは絶縁性がほぼ確保されているので、高周波では絶対的な地位を確保していますが、残念ながら Is(飽和磁化)が低く、また薄膜材料の合成技術がもう一歩、なので、何とか上記の材料の電気抵抗を上げたいところです。
実は、この夢に近いグラニュラー構造というものが実現されています。しかし、電気抵抗はアモルファス金属よりも数桁高いが絶縁物とは言い難い、また、薄膜でしか実現できない、という問題があります。以下にグラニュラー構造の薄膜材料を説明しますが、これをどうやって、バルク(薄帯)で実現するか、成功すれば、一躍、軟磁性材料の雄に躍り出ます。考えてみてください。
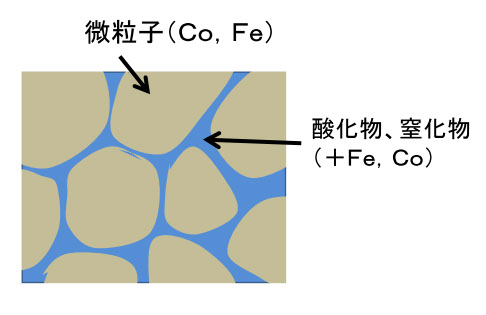
図5-22
図5-22は、グラニュラー構造の模式図です。ナノサイズの微粒子の間に介在物があり、これが高い電気抵抗を持つので、薄膜としての固有抵抗が数μΩm~数10μΩmと、アモルファス材料(~1.5μΩm)の数倍~数10倍になります。この介在物は主に酸化物、窒化物ですが、磁性原子も含むので、微粒子の間の磁気的結合(交換結合)も媒介し、ナノクリスタルと同じように結晶磁気異方性が消失し、軟磁性になります。
Co-Al-Oを原料としてスパッター法で薄膜を作ると、AlはOと結びつきやすい(酸化しやすい)ので、Coのナノ粒子がAl-O層でで囲まれた構造ができる。Al-OにはCoが残留して、Co微粒子間の交換結合を媒介し、軟磁性になっています。
同じ理屈で、沢山のグラニュラー薄膜が作られました。グラニュラー膜のもう一つの特徴は、薄膜形成過程、または熱処理で磁界を印加すると、Co粒子の交換結合が異方的になり、磁界方向を容易軸とする強い一軸磁気異方性(Co系アモルファスのHk = 1200 A/m に対して、Co系グラニュラーは Hk = 8KA/m~80KA/m)が誘起されることです。この磁気異方性の原因は、いまだに明確になっていませんが、もともと、アモルファス、ナノクリスタル、グラニュラー構造は、平衡状態図には無い準安定状態で、熱処理によって相分離が進み(介在物が磁性を失う)、さらに結晶成長が起こることになります。この準安定状態で磁界中熱処理をすると、異方的な構造が起こりそうです。たとえば、介在物中の磁性原子の密度が偏る、あるいは、微粒子間の交換結合が異方的になる、などが考えられます。が、最終結論になりそうな実験検証はありません。で、グラニュラー薄膜の特徴は、
「グラニュラー構造では、非常に強い誘導磁気異方性があり、電気抵抗も数桁高いので、高い共鳴周波数、低い渦電流が実現できる。」 ということ、以下がその例です。
Co-Al-O薄膜(参考文献5-26)
Is = 1.1 Tesla, σ(固有抵抗)= 5.12μΩm, Hk = 8000 A/m
この強い誘導磁気異方性が、グラニュラー薄膜の磁気共鳴周波数を一段と高くしていて、高透磁率薄膜としての周波数範囲が高いほうへ広がっています。詳細は第6章の薄膜の透磁率を見てください。
グラニュラー構造は、薄膜の形でしか実現されていません。薄帯にしたいところですが、金属と酸化物の溶融体を作ることができないので、急冷ロール法では無理です。プラズマジェットや、レーザーアブレーションなど、ガス状態からの急冷であれば、あるいは可能かもしれませんが、筆者の知識では、これ以上何とも言えません。誰か挑戦してくれんか、と思いますが、コストの問題もあるので、相当にchallengingな課題ではあります。
以上の軟磁性材料の飽和磁化、Hkなどの、透磁率、磁気共鳴周波数を決定する定数については、第6章で高周波特性に関連してまとめられています。
なお、微結晶軟磁性材料については、以下に詳しい解説があります。
島田:連載講座 軟磁性材料 ナノ構造材料Ⅱ「ナノクリスタル材料・グラニュラー薄膜」
日本磁気学会 「まぐね」 (Magnetics Japan) 4(11),544-551, 2009
▲ページ上部へ